Михаил Шустов, г. Томск
Произведен анализ пределов применимости закона Мура, характеризующий развитие электронной техники по законам геометрической прогрессии. Сделан вывод о том, что границы применимости этого закона давно преодолены. Приведено уравнение, характеризующие закон развития любых объектов во времени, показана возможность определения вида зависимости развития объекта и прогноза последующего развития процесса во времени.
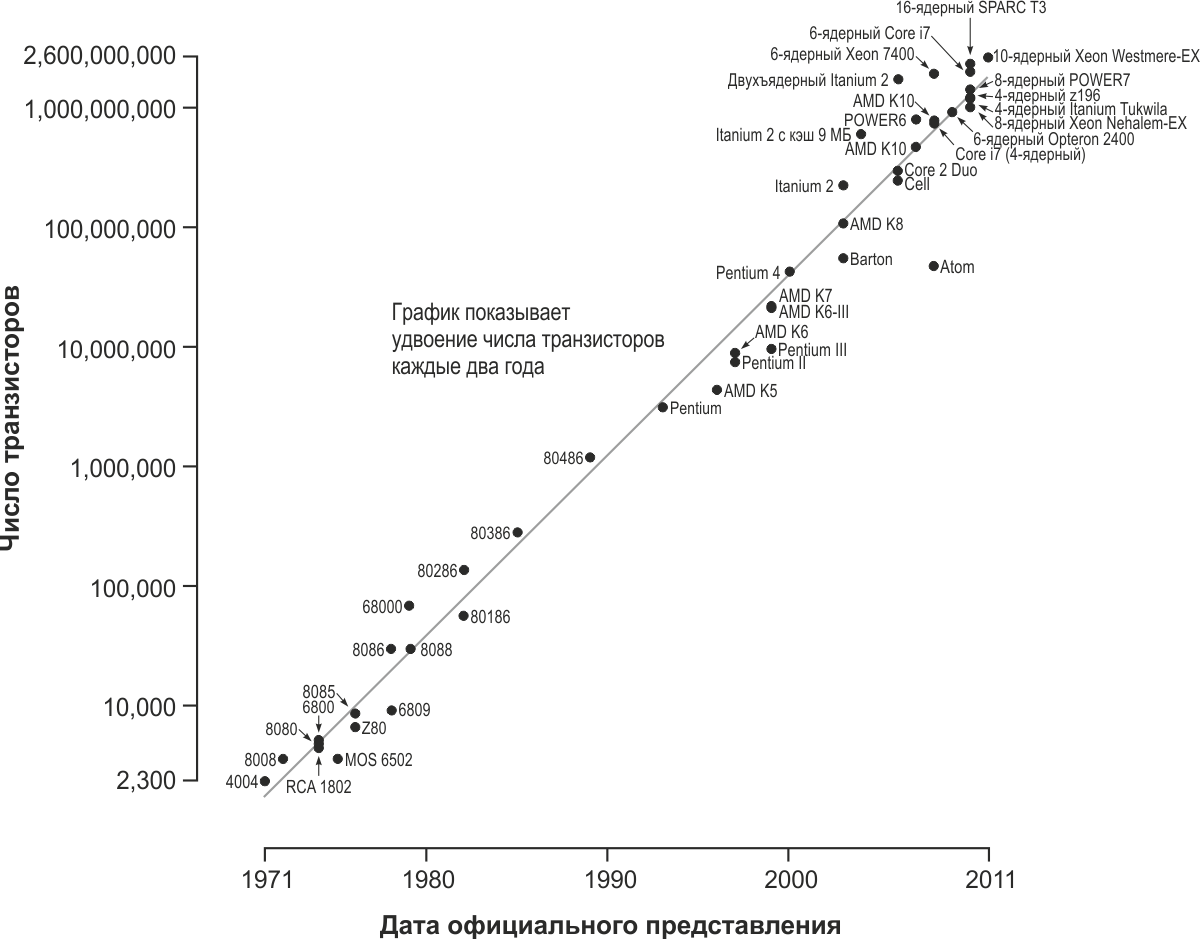
В 1965 году американский бизнесмен и предприниматель Гордон Эрл Мур (Gordon Earle Moore, 1929–), Рисунок 1, один из основателей компании Intel, в ходе подготовки к докладу «Будущее интегральной электроники» выявил закономерность: «Число компонентов на чипе удваивается каждый год», Рисунок 2. Эта закономерность, точнее эмпирическое наблюдение, получило впоследствии наименование «Закон Мура» и позволило прогнозировать развитие электронной техники на грядущие годы.
 |
||
| Рисунок 1. | Гордон Эрл Мур. (Фото: [1]). | |
Уже через 10 лет «закон» пришлось корректировать: удвоение числа транзисторов в кристалле микропроцессора по независящим от законодателя причинам стало происходить не реже, чем раз в два года, а прогноз коллеги Г. Мура по компании Intel Давида Хауса (David House, 1943–) говорил о том, что производительность процессоров должна удваиваться каждые полтора года.
 |
||
| Рисунок 2. | Рост числа транзисторов на кристалле микропроцессора по годам; спрямление графика обусловлено использованием полулогарифмической шкалы. (Источник: [2]). |
|
В 2003 г. Гордон Мур заявил, что экспоненциальный рост физических величин в течение длительного времени просто невозможен [3]. Еще через 4 года Мур наконец-то признал, что закон, названный его именем, скоро перестанет действовать из-за «атомарной природы вещества и ограничения скорости света».
В своих прогнозах развития техники Гордон Эрл Мур не был первым: еще в 1873 г. немецкий философ Фридрих Энгельс в своем незавершенном труде «Диалектика природы» заметил, что развитие науки ускоряется пропорционально квадрату времени, прошедшего от момента ее возникновения.
Следует сказать, что подобные законы могли родиться только в головах людей, не очень хорошо знакомых с основами математики, а именно, с сутью геометрических прогрессий. Хотя оговоримся: на очень узком отрезке времени такие «законы» могут быть правомочны.
Несостоятельность закона Мура будет очевидна, если вспомнить древнюю притчу про мудреца, который изобрел шахматы. Согласно легенде, мудрец попросил у правителя страны «скромное» вознаграждение: за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую – два, за третью – четыре и т. д. В итоге оказалось, что необходимое для оплаты количество зерна намного превышает весь урожай пшеницы, собранный за всю историю человечества. Можно привести и более живой пример – небезызвестная россиянам финансовая пирамида МММ и ее скоротечный крах.
Между тем, развитие любого объекта, в том числе технических систем во времени подчиняется более общим, более фундаментальным законам природы – законам диалектики, сформулированным еще в XVIII–XIX столетиях отцами немецкой философии Иммануилом Кантом и Георгом Гегелем. В осовремененном звучании это Закон единства и борьбы противоположностей, Закон перехода количественных изменений в качественные и Закон отрицания отрицания. Суть их излагать не будем, они общеизвестны, отметим лишь, что эти законы описывают, как это принято у философов, на словах то, что в физике и математике принято выражать строгими математическими формулами.
В математической форме закон развития степени совершенства любого технического объекта во времени можно описать при помощи достаточно универсальной формулы, полученной автором в 1979 году [4-6]:
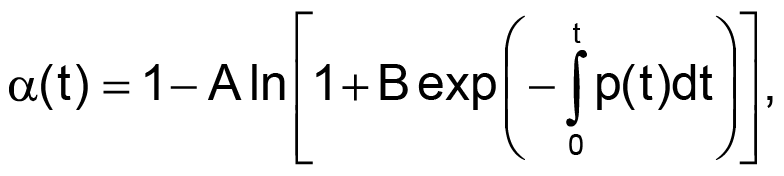
где
α(t) – степень изменения (совершенствования) объекта в пределах от 0 до 1,
A и B – взаимосвязанные нормировочные коэффициенты,
p(t) – закон развития процесса.
При определенных приближениях приведенное выше уравнение преобразуется:
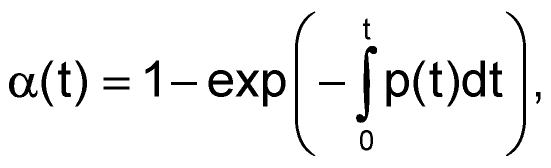
и, в частном случае, при p(t) ~ ts, переходит в уравнение типа:
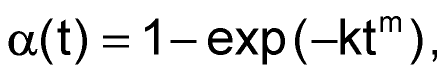
хорошо известное, как уравнение Ерофеева-Колмогорова.
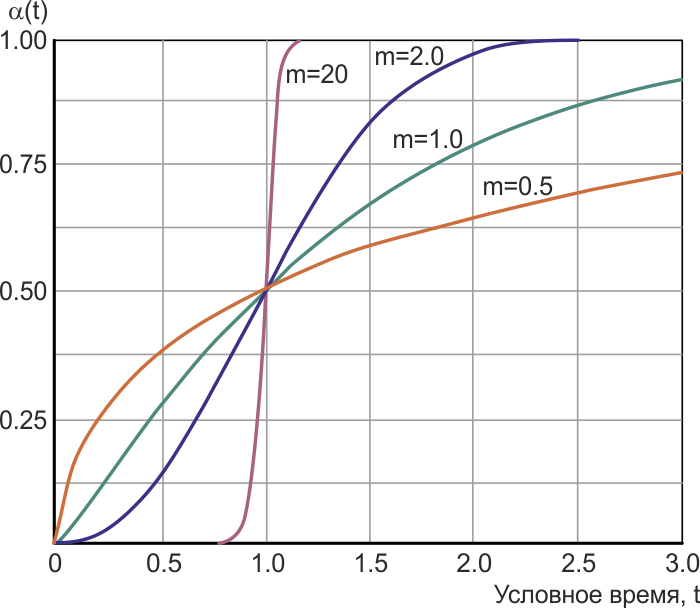
На Рисунке 3 представлена нормированная S-образная кривая степени совершенствования конкретного технического объекта во времени, описываемая приведенной выше формулой для различных показателей степени m.
 |
||
| Рисунок 3. | Внешний вид кривых развития объекта во времени при варьировании показателя степени m. |
|
При дальнейших упрощениях на кривых, приведенных на рисунке, можно найти участки, соответствующие линейному, квадратичному или иному закону развития системы, но справедливость таких приближений будет приемлема лишь на узких интервалах времени.
Отметим, что для закона Мура m = 2, стремительный рост кривой возможен лишь на ранних стадиях процесса. В любом случае, независимо от значения показателя m, кривая развития объекта рано или поздно выйдет на стационарное значение, обусловленное теми или иными объективными причинами.
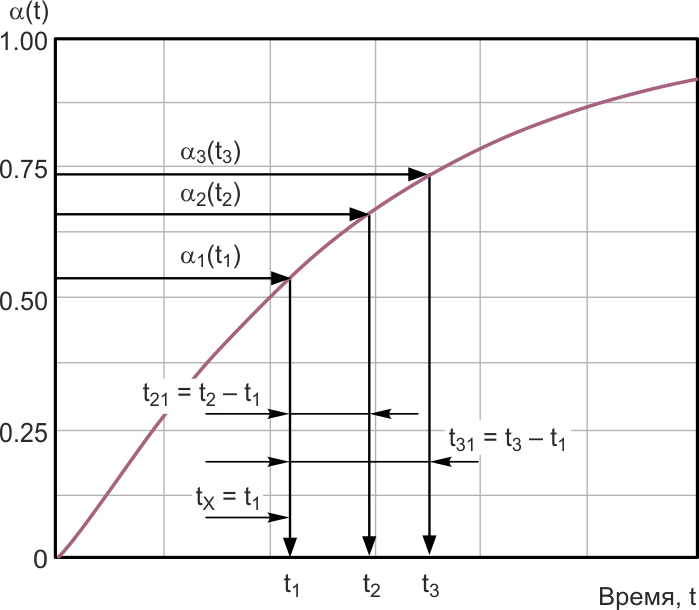
Для ретроспективного анализа или, напротив, прогноза развития процесса во времени по зависимостям, приведенным на Рисунке 3, может быть использован метод трех точек [4]. Следуя логике этого метода, производят три разнесенных во времени определения степени развития (преобразования) системы, Рисунок 4.
 |
||
| Рисунок 4. | Определение степеней развития объекта во времени по трем точкам. |
|
На основании приведенных выше уравнений несложно получить следующие выражения для вычисления давности события tX, а также коэффициента k:
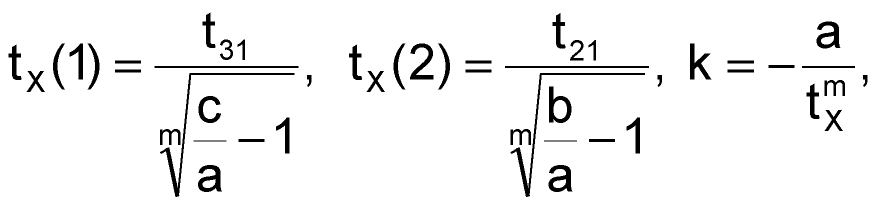
где
a = ln[1 – α1(t1)],
b = ln[1 – α2(t2)],
c = ln[1 – α3(t3)]
– координаты трех точек на Рисунке 4 (нормированные значения количественных изменений системы для трех моментов времени).
Используя систему уравнений для метода трех точек, можно построить графические зависимости tX(m) – кривые tX(1) и tX(2). Точка пересечения кривых дает сведения о «возрасте» процесса и о значении показателя степенной зависимости m. На основании вычисленных значений tX и m может быть определен и коэффициент пропорциональности k.
Наиболее просто задачу установления давности события, определения вида и хода последующего развития процесса можно решить методом последовательных приближений, либо графическим методом.
Для тех, кто не любит математику. Вернемся к закону Мура и попробуем решить задачу проще, по Рисунку 3. Учитывая, что для закона Мура на определенном его участке (ориентировочно за период 1965–2003 гг.) выполнялся показатель степени m = 2, по рисунку определим «текущие координаты» процесса развития. С учетом начала выхода кривой на насыщение это будет точка, отвечающая a(t) = 0.69 и условному времени t = 1.25. Тогда, «цена деления» (t = 1), будет равна (2003–1965)/1.25 = 30.4 лет. Отсюда значение времени t = 2, отвечающие почти полному прекращению роста, будет равно 60.8 лет от начала точки отсчета, что соответствует 2026 году.
Однако пессимистический вывод делать рано, означенная дата будет лишь констатировать факт исчерпания возможности совершенствования данного объекта в силу технологических или иных ограничений. Развитие техники пойдет по иному витку или направлению, с использованием новых технических достижений и научных открытий.
Литература
- Закону Мура – 40 лет!
- Microprocessor Transistor Counts 1971-2011 & Moore's Law.
- Moore G.E. No exponential is forever: but «Forever» can be delayed! // Solid-State Circuits Conference, IEEE International Digest of Technical Papers – 2003. – Vol. 1. – Pp. 20–23.
- Шустов М.А., Кучеренко И.В. Определение вида кинетической кривой и установление давности события методом трех точек // Известия Томского политехнического университета. – 2001. – Т. 304. – Вып. 1. – С. 114–117.
- Шустов М.А. Методические основы инженерно-технического творчества. – М.: НИЦ ИНФРА-М, 2015–2017. – 128 с. (I–III изд.).
- Шустов М.А. Кинетика и формулировки законов фотохимических превращений // Известия Томского политехнического университета. – 2001. – Т. 304. – Вып. 1. – С. 117–122.