Фильтрация часто встречается в аналоговом мире. К сожалению, в цифровом мире инженеры применяют ее в основном к DSP (процессорам обработки цифровых сигналов), а не к небольшим 8-разрядным микроконтроллерам, которые обычно используют разработчики. Такая ситуация возникает из-за того, что математика для проектирования фильтра сложнее той, с которой готово иметь дело большинство инженеров. Кроме того, цифровая фильтрация требует вычислений над целыми числами, а не над числами с плавающей точкой. Из-за этого возникают две проблемы. Во-первых, ошибка округления из-за ограниченного числа битов может ухудшить отклик фильтра или даже сделать его нестабильным. Во-вторых, для обработки дробных значений необходимо использовать целочисленную математику.
Существует несколько способов решения этих проблем. Например, можно использовать операции с 16-, 32- и 64-разрядными числами или масштабировать их для повышения точности. Эти и другие способы обычно требуют больше памяти, и в результате программа часто не помещается в небольшой микроконтроллер. Поиск в литературе показывает, что опубликованные прошивки для цифровых фильтров написаны на языке C. Для программ на C требуется больше памяти, чем для программ, написанных на ассемблере. Это часто делает их неприемлемыми для небольших микроконтроллеров с ограниченными ресурсами памяти.
Листинг, который доступен для скачивания в разделе Загрузки, демонстрирует простой инженерный метод программирования прошивки однополюсного цифрового фильтра нижних частот для 8-битных микроконтроллеров. Программа на ассемблере написана для бюджетного микроконтроллера MC68HC908QT2, но эту идею можно применить к микроконтроллеру любого типа, поскольку в ней используются только стандартные инструкции ассемблера.
Оставляя в стороне сложные методы проектирования, основанные на Z-преобразовании с его громоздкой математикой, эта идея использует другой подход, основанный на рекурсивном уравнении. Каждая выборка выходного сигнала вычисляется как сумма входного сигнала и предыдущей выборки выходного сигнала с соответствующими коэффициентами. Рекурсивное уравнение определяет однополюсный фильтр нижних частот как:
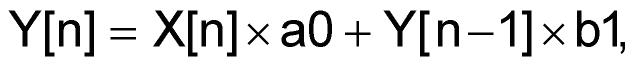
где
X[n] и Y[n] – входные и выходные значения выборки [n],
Y[n–1] – выходное значение предыдущей выборки [n–1],
a0 и b1 – весовые коэффициенты, уменьшающие δ.
Коэффициенты имеют значения 0 < δ < 1, a0 = 1 – δ и b1 = δ. Физически δ – это величина, на которую спадает сигнал между соседними выходными выборками. Значение δ можно задать напрямую или найти его из требуемой постоянной времени фильтра d, которая представляет собой количество выборок, необходимых для того, чтобы выходной сигнал достиг 63.2% от установившегося уровня для фильтра нижних частот. Между d и δ существует жесткая зависимость:
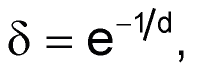
где e – основание натурального логарифма. Предыдущие уравнения дают
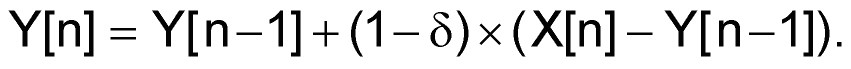
Вместо умножения на число с десятичной точкой 1–δ при программировании на ассемблере удобнее делить на взаимно обратное целое число F:
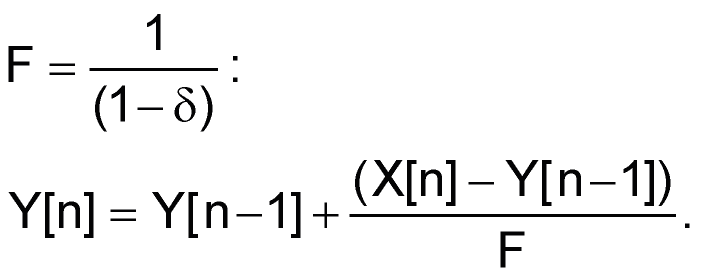
Таким образом, определить параметры цифрового фильтра можно, выполнив следующие шаги:
- Выберите параметр F. Для ассемблера удобно выполнять деление путем сдвигов вправо. Для сдвигов вправо значение F должно быть равно 2S, где S – количество сдвигов. Пусть значение F, достигнутое после трех сдвигов вправо, будет равно 8.
- Рассчитайте декремент
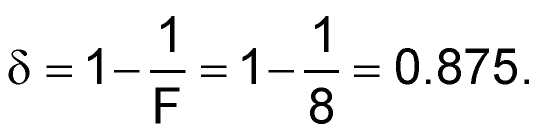
- Рассчитайте постоянную времени как
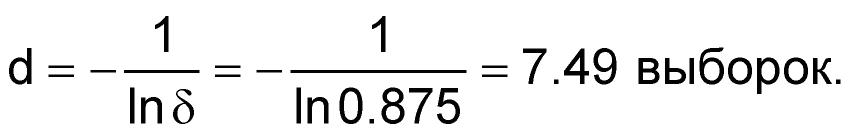
Формула
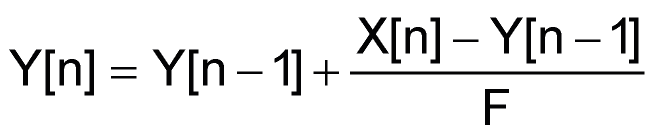
определяет конструкцию фильтра, реализуемого алгоритмом микроконтроллера. Для алгоритма нужны три регистра: входной для X[n], выходной для Y[n] и регистр приращений для хранения члена
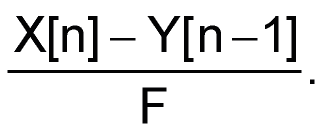
Размеры этих регистров зависят от входных сигналов. В этом приложении сигналы от встроенного 8-разрядного АЦП находятся в диапазоне от 00 до $FF и должны проходить через фильтр нижних частот. Таким образом, входной и выходной регистры имеют размер 1 байт. Чтобы повысить точность деления, к делимому прибавляют половину делителя. Это увеличивает регистр приращения до 2 байт.
Численное выполнение функции фильтрации обеспечивает преимущество постоянства, поскольку допуски компонентов, температурный дрейф и старение не влияют на алгоритм работы фильтра. Реализация цифрового фильтра в микроконтроллере дает дополнительное преимущество в виде гибкости настройки параметров фильтра, поскольку эта гибкость зависит только от прошивки.


 Купить MC68HC908QT2 на РадиоЛоцман.Цены
Купить MC68HC908QT2 на РадиоЛоцман.Цены


