Увеличение разрешения АЦП
Во многих электронных устройствах есть один или несколько АЦП для считывания различных сигналов и напряжений. Часто эти АЦП входят в состав используемого микроконтроллера. Это означает, что, выбрав микроконтроллер, вы определяете максимальное разрешение (рассчитанное на основе разрядности АЦП и величины опорного напряжения), которым вы будете располагать для считывания показаний.
Что произойдет, если на более поздних этапах проектирования вы обнаружите, что вам требуется немного большее разрешение АЦП? Не волнуйтесь, есть несколько простых способов улучшить разрешение дискретизируемых данных. Один из методов я рассматривал в предыдущей статье [1], в которой говорилось об изменении опорного напряжения, поэтому здесь я его обсуждать не буду. Другой способ улучшения разрешения – использование концепции передискретизации.
К вашему сведению: формальное определение передискретизации – это дискретизация с частотой, превышающей частоту Найквиста. Поскольку критерий Найквиста – это дискретизация с частотой, «чуть превышающей» интересующую частоту, это определение довольно расплывчато. Как правило, для базовой дискретизации инженеры используют частоту, в 3–5 раз превышающую частоту Найквиста, и обычно не считают это передискретизацией.
Простая версия передискретизации
Давайте сначала рассмотрим метод, который, по сути, является упрощенной версией передискретизации… – усреднение. (Большинство разработчиков встраиваемых систем используют усреднение для улучшения результатов, стремясь иногда минимизировать влияние неточных показаний и не думая об улучшении разрешения).
Итак, предположим, вы снимаете показания с датчика температуры один раз в секунду. Теперь, чтобы получить более точное разрешение по температуре, снимайте показания каждые 500 мс и усредняйте два показания. Это даст вам еще ½ бита разрешения (математику мы покажем позже). Давайте пойдем дальше – будем снимать показания каждые 250 мс и усреднять четыре результата измерений. Это даст вам целый бит дополнительного разрешения.
Если у вас есть 8-битный АЦП, масштабированный для измерения в диапазоне от 0 до 255 градусов с разрешением 1 градус, то теперь у вас будет виртуальный 9-битный АЦП, способный выдавать показания от 0 до 255.5 градусов с разрешением 0.5 градуса. Усреднив 16 показаний, из 8-битного АЦП вы создадите виртуальный 10-битный АЦП. 64-кратное усреднение показаний позволит создать 11-битный виртуальный АЦП, улучшив ваш 8-битный АЦП тремя дополнительными битами, что даст разрешение в 1 часть на 2048 (или, в примере с датчиком температуры, около 0.12 градуса).
Формула для усреднения
Формула для определения дополнительных битов в зависимости от количества усредненных выборок:
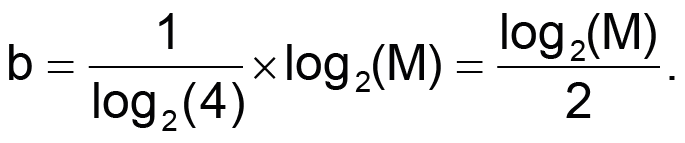
Здесь
M – количество усредненных выборок,
b – количество созданных виртуальных битов, M = 4b.
Если вы хотите найти b при заданном M: b = log4(M).
Возможно, вы ломаете голову, задаваясь вопросом, откуда взялась эта формула. Для начала давайте подумаем о показаниях, которые мы усредняем. Они состоят из двух частей. Первая часть – это истинные, чистые показания, которые пытается выдать нам датчик. Вторая часть – это шум, который мы улавливаем от посторонних сигналов в проводах, источниках питания, компонентах и т. д. (Эти две части сигнала объединяются аддитивным образом).
Будем считать, что этот шум является гауссовым (распределенным статистически нормально; часто изображается в виде колоколообразной кривой; иногда называется белым шумом) и не коррелирует с нашей частотой дискретизации. Теперь, при усреднении, мы сначала суммируем показания. Чистые показания датчика, очевидно, будут суммироваться обычным математическим способом. Что же касается шумовой составляющей, то стандартное отклонение суммы равно квадратному корню из суммы стандартных отклонений. Другими словами, чистая часть увеличивается линейно, а шумовая часть увеличивается как квадратный корень из числа показаний.
Это означает, что не только повышается разрешение, но и в M/√M раз улучшается отношение сигнал/шум, что математически сводится к √M. Проще говоря, усредненное отношение сигнал/шум улучшается в квадратный корень из числа усредненных отсчетов. Таким образом, если мы снимем четыре показания, среднее значение отношения сигнал/шум улучшается в 2 раза, или на эквивалент еще одного бита в АЦП (8-битный АЦП работает как 9-битный АЦП).
Вся эта концепция может выглядеть по-другому, но вы, вероятно, изучали ее на уроках физики или статистики. Там учили, что для получения еще одной значащей цифры необходимо усреднить 100 показаний. Это то же самое, только вы работаете в системе счисления с основанием 10, а не 2.
Недостатки усреднения
Я использовал усреднение во многих прошивках, но это не всегда лучшее решение. Как уже говорилось ранее, линия подключения датчика передает на АЦП хороший сигнал с добавлением некоторого количества помех. Простое усреднение не всегда является лучшим подходом. Одной из проблем является медленный спад в частотной области. Кроме того, затухание в полосе заграждения не очень хорошее. Обе эти проблемы указывают на то, что усреднение позволяет значительной части шума проникнуть в ваш сигнал. Таким образом, возможно, мы и увеличили разрешение считывания, но не удалили из сигнала все возможные шумы.
Снижение уровня шума
Чтобы уменьшить этот шум, распределенный по всему спектру частот сигнала, приходящего по проводам от датчика, можно пропустить сигнал через фильтр нижних частот (ФНЧ). Это может быть сделано с помощью аппаратного ФНЧ, расположенного перед АЦП, или цифрового ФНЧ, включенного после АЦП, или и того, и другого. (Передискретизация упрощает разработку таких фильтров, поскольку спад может быть менее крутым).
Существует множество типов цифровых фильтров, но два основных – это фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ). Я не буду здесь вдаваться в подробности этих фильтров, а лишь отмечу, что их можно проектировать, используя компромиссы между полосой пропускания, крутизной спада, уровнем пульсаций, фазовым сдвигом и т. д.
Более продвинутый подход к передискретизации
Итак, давайте рассмотрим проект создания более совершенной системы передискретизации. На Рисунке 1 показана типичная блок-схема более «формальной» и более качественной системы передискретизации.
 |
|
| Рисунок 1. | Типичная блок-схема передискретизации с антиалайзинговым фильтром, АЦП, цифровым ФНЧ и прореживанием (понижающей дискретизацией). |
Мы начинаем с фильтрации входящего сигнала с помощью аппаратного аналогового фильтра нижних частот (часто называемого антиалайзинговым фильтром). Этот фильтр обычно предназначен для фильтрации входящего полезного сигнала на частоте, чуть превышающей интересующую нас частоту.
Примечание: фильтр сглаживания, расположенный рядом с входом АЦП, на рисунке не показан, но является хорошим конструктивным дополнением. Конденсатор в этой RC-цепи обеспечивает заряд для поддержания уровня напряжения, когда АЦП производит выборку входного сигнала. Подробнее об этом можно узнать в статье «Пример разработки драйвера АЦП, оптимизирующего гармонические искажения, шум и отношение сигнал шум для измерительных приборов с широким динамическим диапазоном» [2].
Затем АЦП дискретизирует сигнал с частотой, в M раз превышающей частоту Найквиста интересующего нас сигнала. После этого поступающий поток выборок снова фильтруется цифровым фильтром нижних частот (обычно КИХ или БИХ) для дальнейшего удаления гауссова шума из сигнала, а также удаления шума квантования, возникающего при работе АЦП. (Для других видов шума, таких как импульсный шум, взрывной шум и т. д., также могут быть полезны иные конструкции фильтров). Передискретизация дала нам преимущество в виде перераспределения шума по широкой полосе частот, и наш цифровой фильтр нижних частот может удалить бóльшую часть этого шума.
Затем мы прореживаем поток данных сигнала. Прореживание (также известное как понижающая дискретизация или децимация) – это просто действие, при котором используется только каждая 2-я, или 3-я, или 4-я выборки, вплоть до каждой M-й, а остальные отбрасываются. Это безопасно благодаря передискретизации и фильтрам нижних частот, поэтому мы не будем сильно искажать сигнал с более низкой частотой дискретизации. Прореживание существенно сужает полосу частот, представленную оставшимися выборками. Дальнейшая обработка теперь требует меньших вычислительных затрат, так как количество выборок значительно сокращается.
Это работает
Это действительно работает. Однажды я занимался проектом, в котором требовался прием очень слабых сигналов, передаваемых по линии электрической сети (меньше 1 Вт). Сигнал ослаблялся конденсаторами на линиях, различными трансформаторами и всеми устройствами потребителей, подключенными к линии сети. Принимаемый сигнал составлял около 10 мкВ и передавался по линии переменного тока 240 В. В итоге мы выполнили передискретизацию примерно в 75 миллионов раз выше частоты Найквиста и смогли успешно принимать сигналы на расстоянии более 160 км от передатчика.