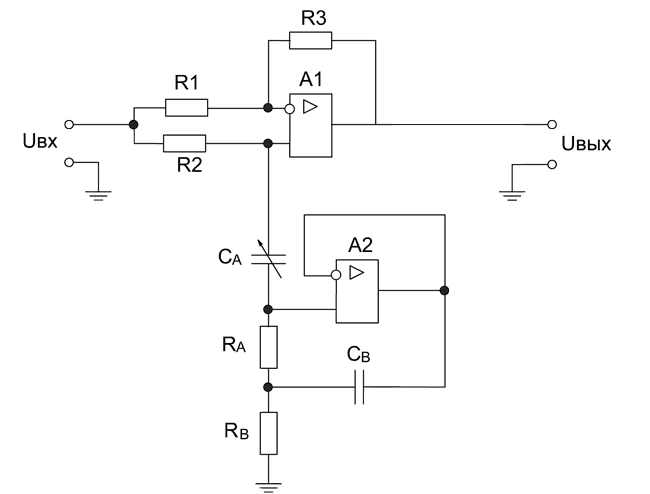
Аналоговый режекторный фильтр может быть создан несколькими способами. С учетом современных тенденций схемотехники, желательна реализация на микроэлементной базе. В связи с этим катушки индуктивности и конденсаторы достаточно большой емкости не должны присутствовать в схеме. В этом случае подойдет схема режекторного фильтра на основе гиратора (Рисунок 9), который благодаря инверсии импеданса позволяет обойтись без катушек индуктивности.
 |
|
| Рисунок 9. | Принципиальная схема режекторного фильтра на основе гиратора. |
Частота режекции здесь равна:
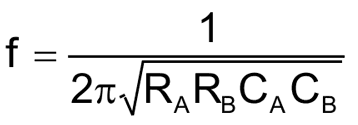 |
(4) |
Если задаться R1 = R3= 500 кОм, R2 = 250 кОм, RA = RB = 100 кОм, CA = 50нФ, f = 2500 Гц, то значение емкости CB, преобразовав (4), можно определить как:
| (5) |
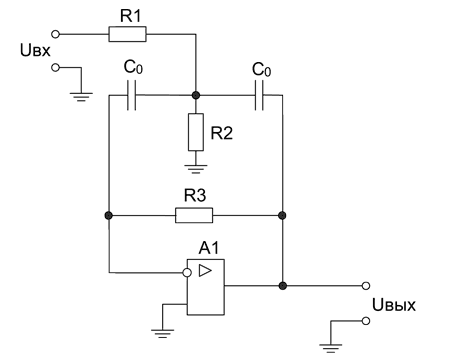
Также существует настраиваемый режекторный фильтр Роберта Пиза, изображенный на Рисунке 10.
 |
|
| Рисунок 10. | Принципиальная схема режекторного фильтра Роберта Пиза. |
Частота режекции для этой схемы равна:
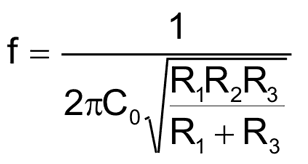 |
(6) |
Аналогично предыдущей схеме, задавшись R1 = R2 = R3 = 100 кОм, f = 50 Гц, преобразовав (6), находим C0 = 46 нФ.
Развитие средств управления выдвигает на передний план задачу цифровой реализации режекторного фильтра. Для этого набором математических выражений надо описать его работу в составе системы управления, которая, в данном случае, является непрерывной, поскольку не содержит нелинейных элементов. В целом, синтез непрерывных систем управления основывается на их описании обыкновенными дифференциальными уравнениями в форме Коши, где, в общем случае, для многомерного элемента каждая входная переменная связана с каждой выходной переменной. Если взаимосвязи по всем каналам линейны или линеаризованы, то в общем случае многомерный элемент можно описать системой неоднородных дифференциальных уравнений. Систему можно записать более компактно в виде одного векторного дифференциального уравнения. Векторное дифференциальное уравнение в форме Коши, отражающее динамические свойства многомерного линейного объекта, является уравнением состояния и используется в качестве математической модели при моделировании методами пространств состояний.
Синтезировать систему можно различными методами, которые делят на две группы: методы численного интегрирования дифференциальных уравнений и матричные методы, основанные на расчете переходной матрицы состояния. Благодаря относительной простоте применения и широкому распространению в литературе чаще используют методы численного интегрирования. При этом, в данном случае, вместо методов численного интегрирования высокого порядка, например метода Рунге-Кутта четвертого порядка или Кутта-Мерсона четвертого порядка, целесообразно применить экономичный, как в плане используемой памяти, так в плане времени выполнения, метод Эйлера первого порядка.
Базовая операция интегрирования, реализованная по методу Эйлера первого порядка, будет выглядеть следующим образом:
| (7) |
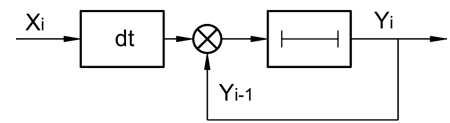
Структурная схема, соответствующая данной операции, представлена на Рисунке 11.
 |
|
| Рисунок 11. | Структурная схема интегратора по методу Эйлера. |
Как видно из формулы (7), при выполнении операции интегрирования основным фактором, влияющим на выходную величину, является шаг дискретизации dt, который в цифровых системах можно определить, считывая один раз за цикл значение таймера. Величина с индексом i определяет сигнал на текущем шаге интегрирования, а с индексом i–1 – на предыдущем.
Поскольку в формуле (1) W(p) представляет собой отношение выходного сигнала Y(p) к входному X(p), то с учетом замены T = ω0(1/Q) получим:
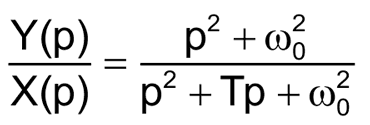 |
(8) |
Произведя несложные математические преобразования, выразим Y(p):
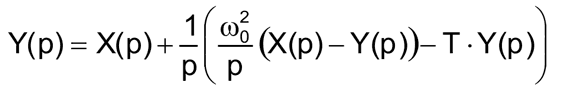 |
(9) |
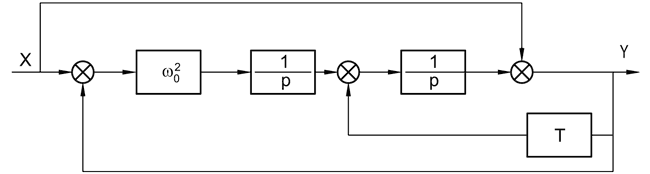
В соответствии с уравнением (9) составим структурную схему (Рисунок 12).
 |
|
| Рисунок 12. | Структурная схема режекторного фильтра. |
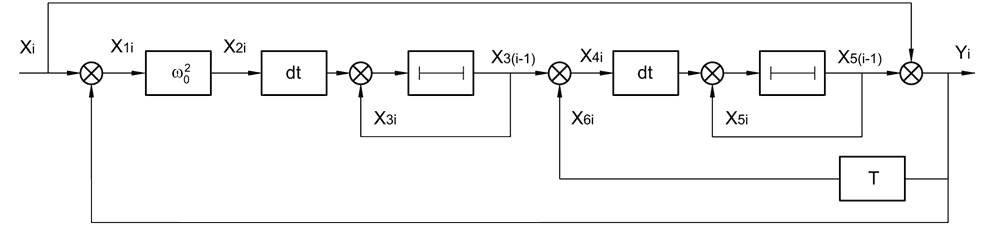
C учетом формулы (7) и Рисунка 11 схема приобретает вид, показанный на Рисунке 13.
 |
|
| Рисунок 13. | Структурная схема режекторного фильтра, расписанная по методу Эйлера. |
На основе полученной структурной схемы составим систему численных выражений, которая будет описывать режекторный фильтр в цифровом виде:
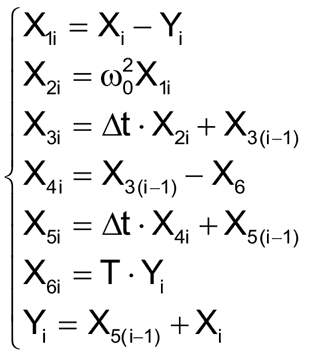 |
(10) |
Как видим, входящие в систему (10) выражения не содержат операций деления, требующих достаточно больших вычислительных ресурсов, поэтому фильтр вполне может быть реализован на маломощных микроконтроллерах.
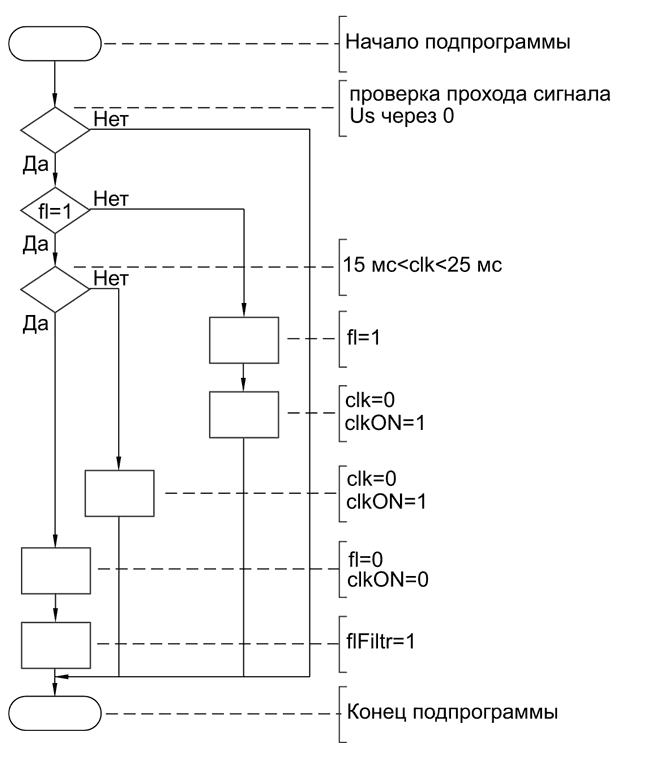
В современных высокопроизводительных цифровых системах управления реализация даже двух режекторных фильтров не является слишком ресурсозатратной задачей. Но в дешевых или старых немодернизированных системах, где используются относительно устаревшие средства вычисления и управления, или устройства с ограниченными вычислительными возможностями, например микроконтроллеры с низкой тактовой частотой, такая задача может повлиять на производительность. В таком случае можно использовать приведенный на Рисунке 14 алгоритм адаптивной фильтрации, который встраивается в основной цикл программы и подключает фильтр лишь при обнаружении помехи. При этом для того, чтобы скомпенсировать «просадку» производительности, на время работы фильтра могут быть отключены какие-либо сервисные функции, например часть интерфейса пользователя.
Данный алгоритм наиболее хорошо подходит для систем, где относительная длительность установившегося процесса существенно больше времени переходных процессов, например, в электроприводах шахтных подъемных установок или конвейеров. В системах с часто меняющимся заданием, например, в исполнительных механизмах промышленных роботов, этот алгоритм будет менее эффективен.
 |
|
| Рисунок 14. | Алгоритм адаптивной фильтрации. |
В приведенном алгоритме выполняется проверка прохода через 0 величины Us, представлящей собой выходной сигнал сумматора, описывающий разность входной величины и сигнала обратной связи. При первом проходе устанавливается флаг fl, а также обнуляется (clk=0) и запускается (clkON=1) таймер clk. При следующем проходе значение clk сравнивается с некоторым диапазоном фильтруемой частоты. Это необходимо, в первую очередь, из-за того, что сигнал Us в установившемся режиме может несколько отличаться от нулевого значения. В данном случае верхняя и нижняя границы диапазона равны 15 и 25 мс, что соответствует частотам 66.67 и 40 Гц. При попадании в этот диапазон сбрасывается fl, отключается таймер и устанавливается флаг включения фильтрации flFiltr, который активирует в основном цикле программы алгоритм режекторного фильтра. Таким образом, не требующий особых вычислительных средств алгоритм может следить за наличием помех на входе системы и лишь при необходимости подключать фильтрацию. Отключение фильтрации можно производить различными способами. Если за системой постоянно следит дежурный персонал, то отключение можно инициировать командой пользователя. В некоторых случаях предпочтительнее использовать таймер, отсчитывающий время, в течение которого производится фильтрация. По истечении этого времени при наличии помехи алгоритм вновь подключит фильтрацию. При определенной интенсивности таких подключений система может счесть помеху постоянной и совсем не отключать фильтрацию.
В работе были показаны методы и способы ликвидации низкочастотных помех в системах автоматического управления электроприводами и исполнительными механизмами. И хотя с подобными помехами на практике приходится сталкиваться не так часто, как с высокочастотными, они также серьезно влияют на работоспособность системы.
Список источников
- Электронные промышленные устройства. М.А. Амелина – г. Смоленск: Московский энергетический институт (смоленский филиал), 2006. – 72 с.
- Проектирование и применение операционных усилителей. Дж. Грэм, Дж. Тоби, Л. Хьюлсмаи – М. : Мир, 1974. – 510 с.
- Операционные усилители и их применение. Ж. Марше – Л. : Энер¬гия, 1974. 215 с.
- Практическая электроника аналоговых устройств. Р. Пиз – М.: ДМК Пресс, 2001. – 320 с.
- Дифференциальное и интегральное исчисления для вузов. Пискунов Н.С. – М.: Наука, 1985. – 432 с.