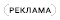Если у вас есть нагрузка с переменным или плохо определенным сопротивлением, и вы хотите регулировать подаваемую в нее мощность (например, нагреватель), простое управление напряжением или током не сработает, поскольку в обоих случаях мощность P = I2R = V2/R зависит от R.
Вместо этого давайте генерировать импульсы с постоянной энергией EPULSE, не зависящей от сопротивления нагрузки RL. Тогда, изменяя частоту f импульсов, мы сможем удобно и точно управлять мощностью нагрузки (P = f·EPULSE) от 0 до известного максимального уровня.
На Рисунке 1а показан простой способ формирования импульса постоянной энергии. Конденсатор C заряжается до начального напряжения V0, накапливая ½CV02 джоулей. Затем он разряжается через нагрузку. Импульс имеет постоянную энергию, которая не зависит от RL.
 |
|
| Рисунок 1. | Импульсы постоянной энергии. |
У такого простого подхода есть недостатки. Во-первых, он расточителен. Для того чтобы зарядить конденсатор энергией ½CV02 джоулей, еще ½CV02 джоулей придется потерять (подробности см. в Приложении). Схема на Рисунке 1б решает эту проблему – все резистивные потери теперь происходят в нагрузке.
Но следует отметить, что распределение мощности импульса весьма неравномерно. Около 63.2% энергии поступает в течение первого интервала ½τ (τ = RL·C; энергия, теряемая в нагрузке, увеличивается в два раза быстрее, чем повышается напряжение, отсюда и коэффициент ½). Для следующих 36.1% энергии требуется еще ½·4τ, что эквивалентно всего лишь примерно 1/7 средней мощности первого интервала ½τ. Неравномерное распределение мощности ограничивает максимальную мощность, которую может контролировать схема. Для передачи оставшихся 0.67% энергии потребуется бесконечное время. На практике этим пренебрегают, что ограничивает точность.
Однако, как показано на Рисунке 1в, можно прерывать зарядку после того, как напряжение на конденсаторе достигнет определенного порогового значения VC. Энергия, рассеиваемая в нагрузке, равна CVC·V0 – ½CVC2 и снова не зависит от величины RL (см. вывод в Приложении).
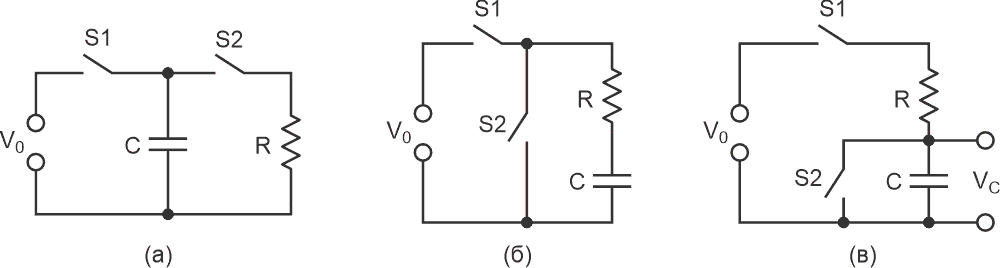
При выборе уровня порога VC основное внимание уделяется выбросам, из-за которых энергия импульса оказывается выше расчетной. Скорость нарастания в момент достижения порога равна
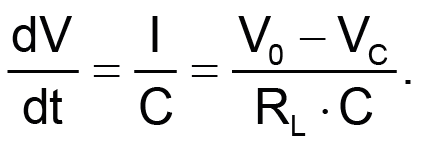
Более низкое значение порога VC увеличивает выброс при том же быстродействии компаратора.
На Рисунке 2 показана одна из возможных реализаций. Микросхема 555 содержит ключи, компаратор и логику. Вход запуска смещен выше порога срабатывания делителем R1-R2. Запускающие импульсы проходят через конденсатор C1 небольшой емкости (2-10 пФ), чтобы предотвратить насыщение компаратора (см. техническое описание микросхемы). Поэтому максимальная рабочая частота сопоставима с частотой генератора.
 |
|
| Рисунок 2. | Базовая реализация схемы постоянной мощности. |
Пороговое напряжение устанавливается делителем R3-R4. Параллельный регулятор TL431 (выбор резисторов R6-R8 см. в техническом описании) устанавливает напряжение зарядки. В зависимости от выбранных номиналов может потребоваться резистор R5 (пара Ом) для предотвращения чрезмерного тока в параллельном регуляторе. Фактическое напряжение зарядки будет выше на величину прямого падения напряжения на диоде D1. Диод D1 должен быть быстрым, а конденсатор C – пленочным.
При использовании более сложной схемы управления можно исключить бесполезный разряд на землю. Например, конденсатор C можно заряжать от –V/2 до +V/2 через нагрузку RL от положительной шины V0 – V/2 и разряжать через RL в отрицательную шину –V0 + V/2, создавая симметричный импульс как для заряда, так и для разряда, и не тратя энергию впустую. В качестве альтернативы можно сделать так, чтобы напряжение на конденсаторе колебалось вокруг средней точки над землей.
Эта конструкция была использована для создания источника питания тепловых МЭМС-датчиков.
Приложение
На Рисунке 3 показана схема, в которой конденсатор заряжается от потенциала V0 до потенциала VC. Заряды, перемещающиеся от более высокого потенциала к более низкому, совершают работу W = q∆V.
 |
|
| Рисунок 3. | Зарядка конденсатора. |
Заряд дискретен, поэтому мы можем рассмотреть вклад каждого отдельного заряда. Такая зарядка начинается из состояния покоя при потенциале V0 и заканчивается при некотором более низком потенциале VC на пластине конденсатора.
Если конденсатор С изначально полностью разряжен, работа, совершаемая каждым зарядом, происходит по следующей схеме:
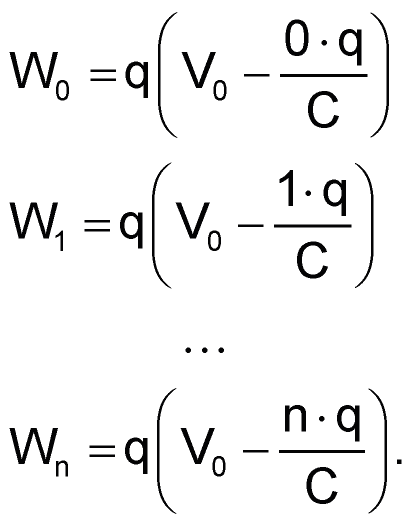
Здесь n·q – общий заряд Q на конденсаторе после поступления n отдельных зарядов, а
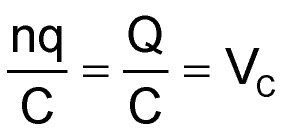
– это напряжение, до которого заряжается конденсатор. Из этого соотношения определяем количество зарядов:
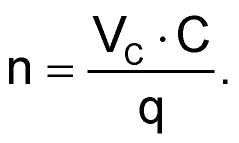
Общая работа равна сумме вкладов каждого заряда: W = W0 + W1 +…+ Wn. Тогда работа W(VC), выраженная как функция VC, равна:
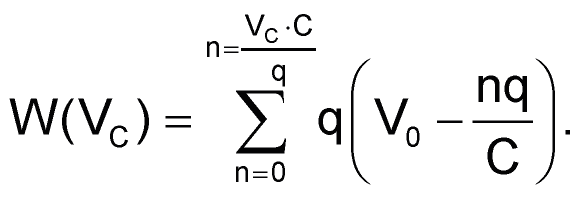
Упрощая, получаем:
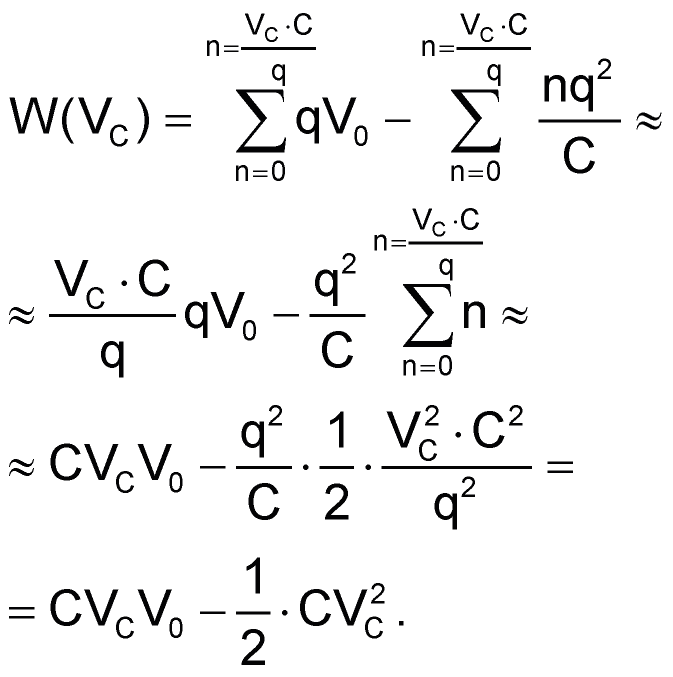
Первая часть последней формулы обозначает энергию, полученную от источника напряжения. Вторая часть – энергия, которую хранит конденсатор, заряженный до напряжения VC. Разность – это потерянная энергия, преобразованная в тепло в нагрузке. Как видно из формулы, она никак не зависит от R.
Если зарядить конденсатор до полного потенциала источника, напряжение VC будет равно V0. Тогда источник отдаст CV02 джоулей, на конденсаторе будет храниться ½CV02 джоулей, и еще ½CV02 джоулей преобразуется в тепло.