Как реализовать цифровую схему управления импульсным преобразователем электрической энергии. Часть 2

Особенности выполнения фоновых операций

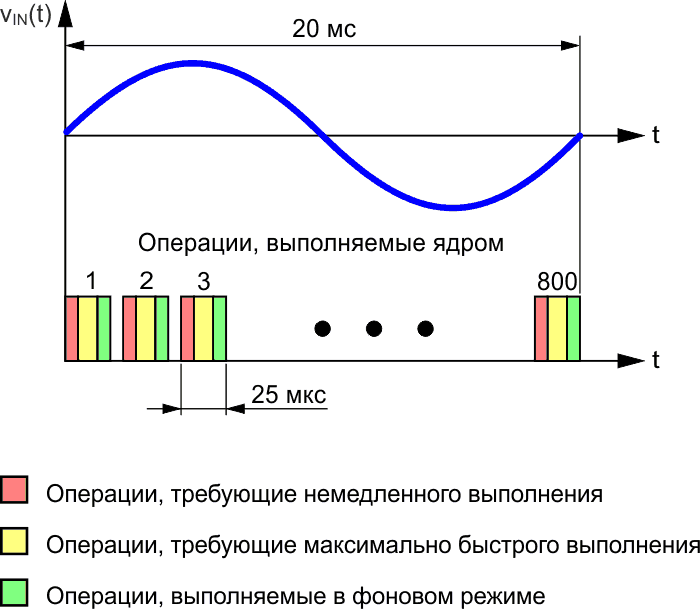
За время одного периода сетевого напряжения продолжительностью 20 мс микроконтроллер стабилизатора GOFER-9000 «просчитывает» около 800 итераций основного цикла, в каждой из которых, в общем случае, могут быть свои фоновые задачи. Например, на первой итерации может происходить расчет средних значений напряжений и токов, на второй – их действующих значений, на 254-ой – контроль температуры и управление вентилятором и так далее (Рисунок 10). В этом случае у программиста возникает задача проверки номера итерации для принятия решения, какой именно код нужно выполнять в данный момент.

Рисунок 10.	Приблизительный план выполнения операций за время периода сетевого напряжения.

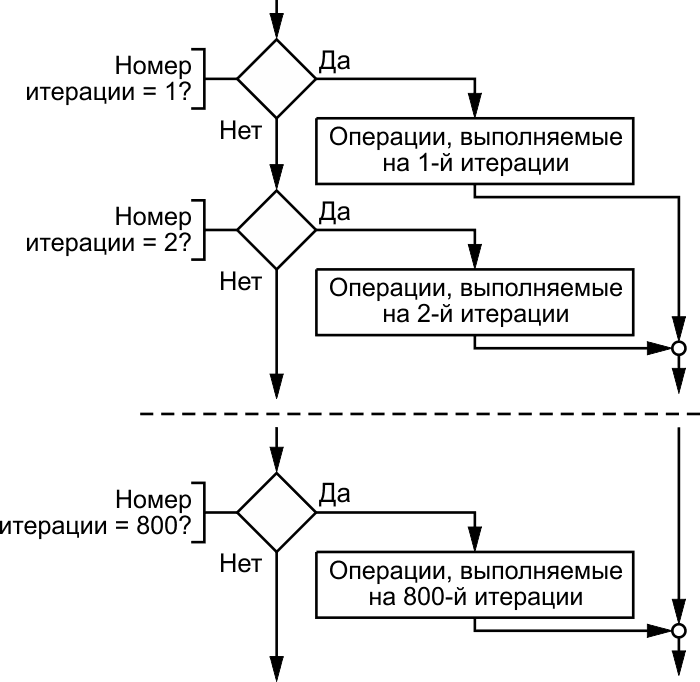
Классический алгоритм решения такой задачи показан на Рисунке 11. На С/С++ его проще всего реализовать с помощью операторов if или switch. Такой подход прост для реализации и понимания, а в сочетании с гибкостью оператора switch, с его помощью можно значительно расширить количество вариантов поведения программы.

Рисунок 11.	Классический алгоритм проверки номера итерации.

Но при этом существует проблема, заключающаяся в наличии затрат процессорного времени на каждую проверку номера итерации. При небольшом количестве вариантов это особо не отразится на скорости выполнения программы. Однако если нужно, например, реализовать все 800 ответвлений, то проверка номера итерации, даже при максимальной тактовой частоте и наивысшем уровне оптимизации, потребует столь большого числа инструкций, что на выполнение полезного кода уже может просто не остаться процессорного времени.

В этом случае лучше всего применить так называемый «эстафетный» метод программирования, когда один блок кода (подпрограмма) по цепочке передает управление другому. В этом случае все фоновые операции «упаковываются» в несколько подпрограмм с одинаковым интерфейсом вызова, то есть, с одинаковым типом возвращаемого значения и одинаковым списком параметров. В данном случае таких подпрограмм будет 800 с названиями, например, «Operations_001» – «Operations_800». Пусть, для простоты, они не будут иметь никаких параметров и ничего не будут возвращать.

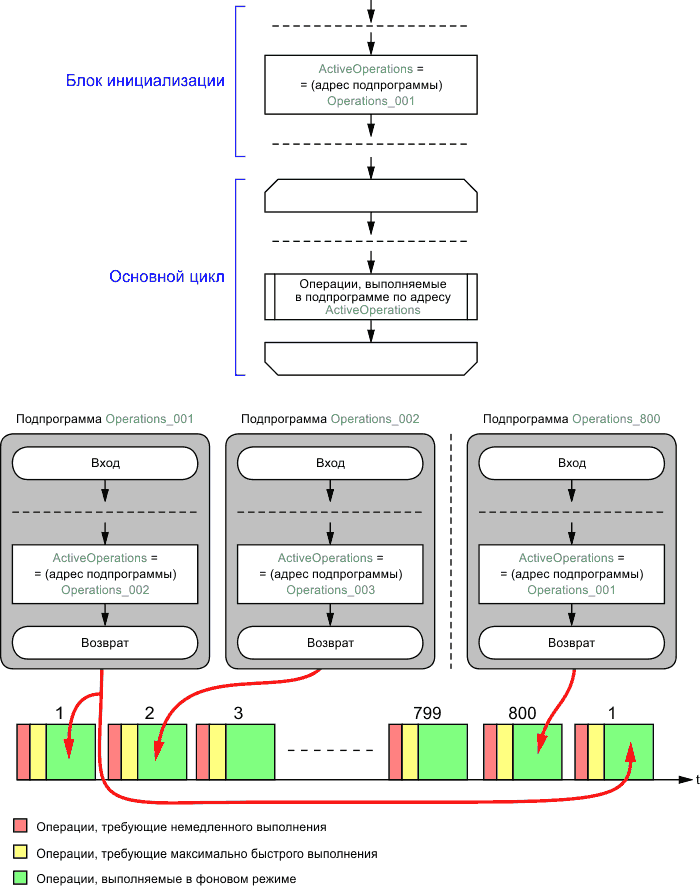
Для выполнения конкретной (одной из восьмисот) подпрограммы в основной программе создается дополнительная переменная типа «указатель на функцию» [7], например, с названием ActiveOperations, в которой будет храниться адрес активной подпрограммы. На этапе инициализации этой переменной присваивается значение первого блока, в данном случае – Operations_001. Инициализация этой переменной является обязательной. Если ее не выполнить, то произойдет переход по случайному адресу, со всеми вытекающими отсюда последствиями в виде неожиданной перезагрузки или зависания микроконтроллера.

Если переменная ActiveOperations правильно инициализирована, то на первом проходе основного цикла будет выполнена подпрограмма Operations_001, внутри которой переменной ActiveOperations будет присвоен адрес следующего блока фоновых операций, в данном случае – Operations_002. На втором проходе основного цикла в переменной ActiveOperations уже хранится адрес подпрограммы Operations_002, поэтому вместо подпрограммы Operations_001 будет выполнен код, содержащийся в подпрограмме Operations_002. А внутри подпрограммы Operations_002 переменной ActiveOperations будет присвоен адрес следующего блока – Operations_003. И так до тех пор, пока внутри 800-го блока (Operations_800) переменной ActiveOperations не будет присвоен адрес первого исполняемого блока (Operations_001). При этом круг замкнется, и все 800 подпрограмм Operations_001 – Operations_800 будут выполнены повторно.

Рисунок 12.	Алгоритм программы при использовании эстафетного метода.

Как видно из алгоритма (Рисунок 12), при использовании эстафетного метода выполнение восьмисот разных вариантов фоновых операций требует минимума затрат процессорного времени на служебные действия. В этом случае в каждой итерации основного цикла необходимо лишь изменить значение одной переменной и вызвать одну подпрограмму. Поскольку переменные типа «указатель на функцию» не слишком часто используются при программировании микроконтроллеров, то для лучшего понимания особенностей этого метода будет полезно изучить исходный код примера подобной программы, написанный на С/С++ (Листинг 1).

Листинг 1. Исходный код реализации алгоритма Рисунка 12

// Объявления переменной ActiveOperations типа «указатель на функцию»
void (*ActiveOperations)(void);
// Блок инициализации
...
ActiveOperations = Operations_001;
...
// Основной цикл
while (IsOK)
{
...
ActiveOperations();
...
}

// Операции, выполняемые на итерации №1
void Operations_001(void)
{
...
ActiveOperations = Operations_002;
}
// Операции, выполняемые на итерации №2
void Operations_002(void)
{
...
ActiveOperations = Operations_003;
}
...
// Операции, выполняемые на итерации №800
void Operations_800(void)
{
...
ActiveOperations = Operations_001;
}

Если фоновые операции в каждой из итераций основного цикла различны, тогда программисту, действительно, нужно реализовать все 800 подпрограмм, что потребует достаточно больших затрат рабочего времени и увеличит размер прошивки. Однако на практике чаще всего оказывается, что основной цикл содержит намного меньше уникального кода. Например, в прошивке стабилизатора GF-9000 таких «ключевых» итераций, четко привязанных к определенным моментам периода сетевого напряжения, оказалось не больше сорока. Все остальное время выполнялись операции, никак не зависящие от времени, например, проверка порта UART, состояния кнопок или отправка данных на индикатор. И хоть количество инструкций, необходимых для сорока проверок, намного меньше, чем для восьмисот, все равно решение данной задачи классическим способом, с помощью оператора switch, привело к резкому увеличению времени выполнения прохода и срабатыванию узла контроля времени выполнения программы (описанного в первой части этой статьи). Поэтому и был использован эстафетный метод, а для того, чтобы не создавать все 800 подпрограмм, была реализована дополнительная проверка текущего номера итерации.

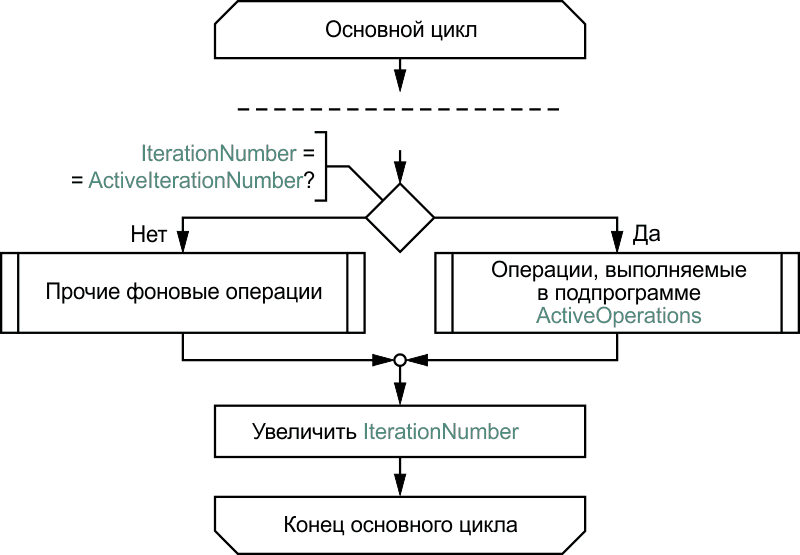
Таким образом, итоговый алгоритм выполнения фоновых операций выглядит следующим образом (Рисунок 13). Так же как и в предыдущем варианте, переменная ActiveOperations типа «указатель на функцию» содержит адрес активной подпрограммы, только подпрограмма эта будет выполнена на итерации, номер которой хранится в переменной ActiveIterationNumber. В этом случае на каждом проходе основного цикла выполняется единственная проверка переменной IterationNumber, содержащей текущий номер итерации. Когда значения, переменных IterationNumber и ActiveIterationNumber совпадают, тогда выполняется подпрограмма Operations_ххх по адресу, содержащемуся в переменной ActiveOperations, а если нет – какие-либо третьестепенные задачи, выполнение которых, кстати, тоже можно организовать по эстафетному методу. Значения переменных ActiveIterationNumber и ActiveOperations изменяются внутри подпрограмм Operations_ххх по правилу, определяемому общей логикой программы.

Рисунок 13.	Комбинированный алгоритм выполнения фоновых операций с использованием «эстафетного» метода.

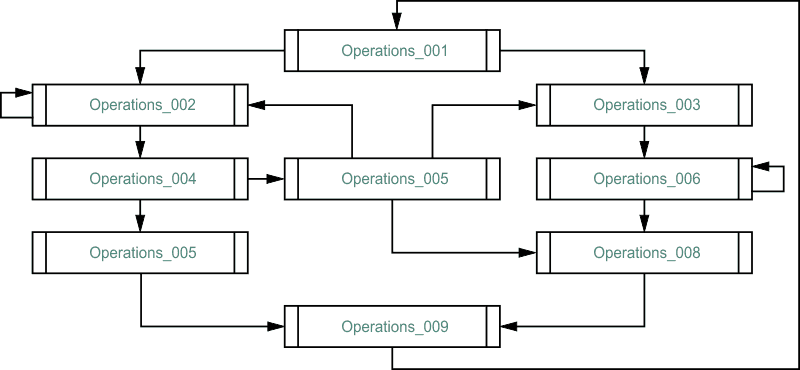
Следует отметить, что эстафетный метод является очень гибким. Он позволяет организовать выполнение подпрограмм Operations_ххх в каком угодно порядке, ведь внутри подпрограммы переменной ActiveOperations можно присвоить любое значение, также как и оставить ее неизменной. Это позволяет реализовывать самые «безумные» переходы (Рисунок 14), например, основанные на текущем состоянии «внешнего мира». Недостатком такого метода является катастрофическое падение уровня читаемости программы и понимания логики ее работы, что требует привлечения, как минимум, опытного программиста, способного удержать в своем воображении все возможные переходы.

Рисунок 14.	Пример алгоритма работы программы, который можно реализовать с помощью эстафетного метода.

Ценой ошибки, которую вряд ли обнаружит даже самый лучший компилятор, может стать абсолютно непредсказуемая работа программы. Ну а если при неправильных значениях указателя ActiveOperations произойдет переход в область кода, отвечающего за алгоритм работы силовых ключей, то подобная ошибка может привести и к выходу из строя силовой части, поэтому этот метод нужно применять с особой осторожностью.

Особенности проверки значения переменных

Во время работы программы необходимо постоянно контролировать значения достаточно большого количества переменных, содержащих информацию о «внешнем» и «внутреннем» мире микроконтроллера. К наиболее важным из них относятся величины входного и выходного напряжений, выходного тока и температуры. В некоторых случаях приходится контролировать мгновенные значения, измеряемые непосредственно АЦП (входное напряжение и выходной ток), а в некоторых – средние и/или действующие значения, получаемые путем математической обработки некоторого количества измерений. В любом случае, где-то в программе необходимо принимать решение о том, находится ли значение данной переменной в допустимых пределах или нет. При этом следует учитывать высокий уровень помех, как поступающих из источника первичного питания, так и создаваемых «своей» силовой частью. В случае стабилизатора, работающего от промышленной сети, высокая помехозащищенность алгоритмов управления является обязательным условием, ведь постоянное срабатывание защиты, например, при включении холодильника, никак не будет способствовать популярности данной техники.

Принятие подобных решений является сложным и болезненным. С одной стороны, необходимо защитить силовую часть от возможного выхода из строя, а с другой – обеспечить максимальную живучесть аппарата в сложных условиях. Существует множество вариантов решения этой задачи, в том числе и аппаратными средствами, например, с помощью компараторов или АЦП с «оконными» функциями, и за все время работы с цифровыми контурами управления было перепробовано достаточно много способов контроля значения переменных, каждый из которых имеет свои достоинства и недостатки. В конечном итоге был выбран один метод, наилучшим образом сочетающий высокую надежность и помехозащищенность.

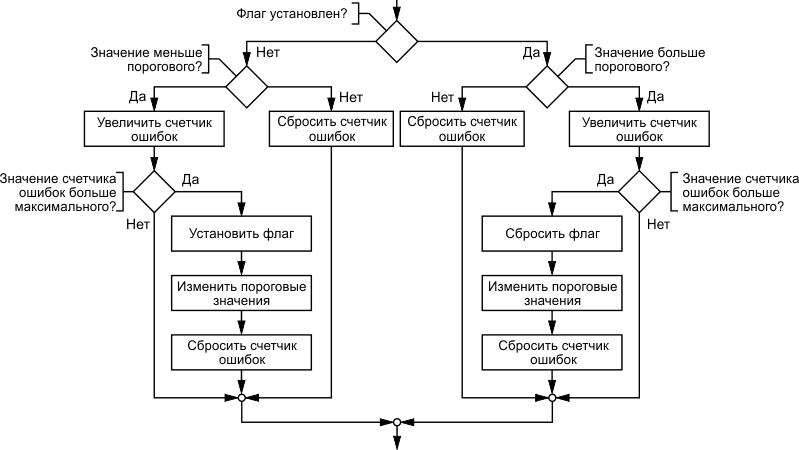
Рисунок 15.	Базовый алгоритм проверки значения переменной.

Базовый алгоритм проверки какого-либо значения при использовании этого метода показан на Рисунке 15. В этом алгоритме осуществляется проверка некоторой переменной (пусть, для определенности, это будет значение температуры) на максимальное значение. Для этого необходимы следующие переменные:

• флаг нормального значения параметра (переменная логического типа True/False);
• пороговое значение параметра;
• счетчик ошибок;
• максимальное значение счетчика ошибок.

Также в программе необходимо определить несколько констант:

• максимальное значение параметра, когда он в норме (порог выключения);
• минимальное значение параметра, когда он за пределами нормы (порог включения);
• максимальное значение счетчика ошибок, когда параметр в норме;
• максимальное значение счетчика ошибок, когда параметр за пределами нормы.

Флаг нормальной работы нужен для быстрой проверки состояния данного параметра. Обычно его значение проверяется на самом верхнем уровне логики программы (например, силовую часть преобразователя можно включить при нормальных значениях входного напряжения и температуры, при этом не важно, чему именно равны входное напряжение и температура, важно, что они в норме).

Разные значения порогов (включения и выключения) необходимы для обеспечения необходимого гистерезиса. Например, для случая температуры порог выключения аппарата (максимальное значение) может быть 85 °C, а порог включения (минимальное значение) – 50 °C.

Счетчики ошибок необходимы для обеспечения требуемого уровня помехозащищенности. Конечно, вопросы противодействия электромагнитным помехам необходимо прорабатывать, прежде всего, на аппаратном уровне. На каждом аналоговом входе должны стоять помехоподавляющие фильтры с ограничителями импульсных напряжений, печатные проводники необходимо разводить с минимальной площадью токового контура, а аналоговая земля соединяться с цифровой только в одной точке. Кроме того, плату управления лучше электрически изолировать от силовой части. Однако в любом случае необходимо помнить, что «против лома нет приема» при появлении высокоэнергетической помехи этих мер может оказаться недостаточно, и помеха, так или иначе, отразится на результатах измерений АЦП.

На этапе инициализации переменным присваиваются некоторые начальные значения, зависящие от конкретной ситуации и параметра. В случае температуры, флаг обычно сбрасывается (параметр не в норме), а пороговому значению присваивается значение порога включения. Счетчик ошибок обычно всегда устанавливается в ноль, а его максимальному значению присваивается значение соответствующей константы.

Основной алгоритм проверки зависит от текущего состояния флага. Если значение параметра в норме (флаг установлен) и его текущее значение не превышает пороговое, то счетчик ошибок сбрасывается. Если параметр не в норме (флаг сброшен), тогда наоборот – счетчик ошибок будет сбрасываться, если текущее значение параметра будет больше порогового значения. Таким образом, счетчик ошибок фактически показывает, насколько новое состояние отличается от текущего. Если текущее состояние («все хорошо» или «все плохо») совпадает с результатами измерений, то счетчик ошибок будет находиться в нулевом состоянии, и флаг меняться не будет.

Однако если новое значение контролируемого параметра больше (флаг установлен) или меньше (флаг сброшен) пороговой величины, тогда счетчик ошибок будет увеличен, после чего его состояние будет проверено на предмет нахождения в допустимых пределах. Если количество ошибок не достигло критического числа, определяемого соответствующей переменной, то ничего не произойдет. А если количество ошибок превысило максимальное значение, тогда осуществится перевод данного программного узла в противоположное состояние: флаг будет инвертирован, пороговые значения изменены, а счетчик ошибок, как обычно, сброшен.

Подобный алгоритм позволяет игнорировать отдельные единичные выходы контролируемого параметра за пределы допустимых значений и значительно повысить устойчивость системы «на границе» допустимых условий эксплуатации. Например, в случае контроля температуры стабилизатора совершенно не обязательно отключать аппарат, если температура достигла максимально допустимого значения. Тепловые процессы инертны и увеличение температуры радиатора транзистора может быть связано с кратковременной нагрузкой стабилизатора в недавнем прошлом, например, с включением электрочайника на несколько десятков секунд. Поэтому, если установить максимальное значение счетчика ошибок таким, чтобы выключение аппарата произошло, например, через одну минуту, то вполне возможно, что температура транзисторов опустится ниже порога раньше, чем счетчик ошибок достигнет максимального значения (особенно если активизировать при этом систему охлаждения). Согласитесь, такой алгоритм намного лучше отключения питания во всем доме через 15 секунд после закипания воды для чая.

Конечно, есть риск, что при больших максимальных значениях счетчика ошибок будет большая задержка и в срабатывании защиты. Например, если в предыдущем примере снова включить электрочайник, то через минуту уже может оказаться поздно что-либо выключать – температура кристаллов транзисторов превысит максимально допустимые значения, при этом счетчик все еще будет считать ошибки. В этом случае счетчик ошибок необходимо увеличивать на значение Δ, зависящее от разницы между текущим и пороговым значением. Обычно используют следующую формулу:

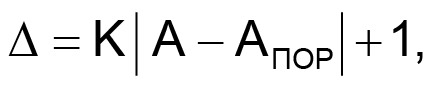(1)

где

А, А_ПОР – соответственно, текущее и пороговое значения измеряемой величины;
К – некоторый коэффициент, подбираемый экспериментально.

При этом нужно не забывать, что переменная счетчика ошибок обычно имеет целый тип, поэтому при использовании формулы (1) следует учитывать специфику целочисленных вычислений.

Например, если для рассмотренного выше случая контроля температуры использовать К = 1/2, а пороговое значение счетчика ошибок выбрать таким, что при его увеличении на единицу аппарат отключится через 60 секунд, то получим следующий алгоритм отключения устройства. Если температура транзисторов не более чем на 2 градуса превышает пороговое значение, то счетчик ошибок при каждой проверке будет увеличиваться на единицу, и аппарат отключится через 60 секунд. Если текущая температура больше пороговой на 3…4 градуса, то счетчик ошибок с каждым разом будет увеличиваться на 2, и аппарат отключится через 30 секунд. Если же текущая температура будет на 20 градусов больше порогового значения, то счетчик ошибок с каждым разом будет увеличиваться на 11, и аппарат отключится меньше чем за 6 секунд.

Как видно из этого примера, цифровые методы управления могут обеспечить гибкость управления, недостижимую при использовании традиционных аналоговых контроллеров. Кроме того, на Рисунке 15 приведена всего лишь базовая версия алгоритма. Но ведь никто не запрещает программисту ее модифицировать в зависимости от конкретной ситуации. Например, добавить проверку не только максимального, но и минимального значения, что обычно необходимо во время контроля мгновенных значений напряжений и токов. Кроме того, совершенно необязательно использовать столь большое количество констант и переменных. Очень часто максимальное значение счетчика ошибок одинаково для любого значения флага, что позволяет исключить соответствующую переменную и использовать всего одну константу.

Кстати, в написании какого-нибудь универсального проверочного модуля, подходящего на все случаи жизни, тоже нет особой необходимости. Практика показывает, что в большинстве случаев программисту проще написать «с нуля» несколько десятков алгоритмов Рисунка 15, чем думать, как «прикрутить» готовый универсальный модуль под конкретную задачу. К тому же использование универсального модуля, скорее всего, потребует дополнительного процессорного времени за счет проведения большего количества внутренних проверок.

Особенности измерения входных сигналов

Мгновенные значения, получаемые непосредственно после оцифровки, в большинстве случаев недостаточно информативны для принятия конкретных решений, поэтому на практике часто возникает задача определения средних и действующих значений измеряемых параметров. Кроме того, АЦП измеряет «в попугаях» – некоторых условных единицах, которые потом необходимо перевести в вольты, амперы или градусы Цельсия.

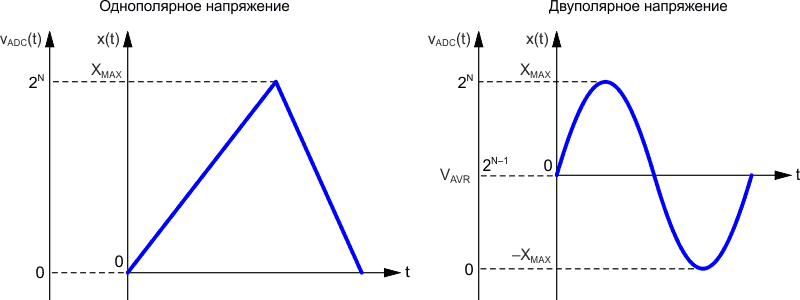
Рисунок 16.	Варианты сигналов на входе АЦП.

При использовании микроконтроллеров общего назначения возможны два варианта входных сигналов: сигнал с однополярным и двуполярным входным напряжением (Рисунок 16). При работе с однополярными сигналами напряжение на входе АЦП пропорционально входному напряжению, поэтому для перевода полученного значения в традиционные вольты или амперы следует воспользоваться формулой:

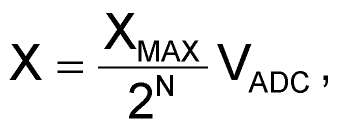(2)

где

V_ADC – результат измерения АЦП (в «попугаях»);
N – разрядность АЦП;
Х_MAX – максимальное измеряемое значение датчика (при котором, АЦП даст результат 2^N);

Отношение Х_MAX/2_N обычно является постоянным, поэтому его лучше вычислить заранее и записать в виде константы в исходном коде программы или в EEPROM.

Очень часто при программировании необходимо решать обратную задачу – определять, какое значение АЦП V_ADC соответствует тому или иному входному напряжению или току X. Такая задача, например, возникает при проверке входного напряжения; при этом совершенно необязательно пересчитывать результат измерения АЦП в вольты или амперы. Достаточно полученный результат измерений АЦП V_ADC сравнить с константами, полученными по формуле:

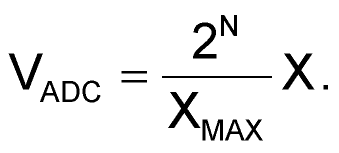(3)

Для двуполярных сигналов соотношения получаются аналогично, за исключением того, что максимальное значение, измеряемое АЦП, будет в два меньше, поскольку из текущего значения результатов оцифровки АЦП необходимо вычесть постоянную составляющую на входе V_AVR:

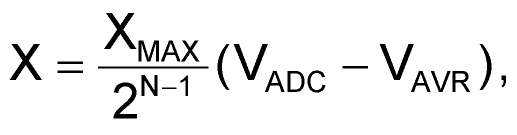(4)

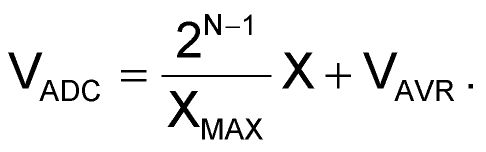(5)

В идеальном случае, при измерении двуполярных сигналов, постоянное смещение на входе АЦП V_AVR должно быть равно половине опорного напряжения АЦП, чтобы при отсутствии входного сигнала результат измерения АЦП был точно равен 2^{N – 1}. Очевидно, что на практике такого никогда не будет из-за технологического разброса компонентов, дрейфа опорных напряжений и прочих «неприятностей реального мира». Поэтому среднее значение V_AVR в формулах (4) и (5) лучше не принимать жестко равным 2^{N – 1}, а измерять по следующей формуле:

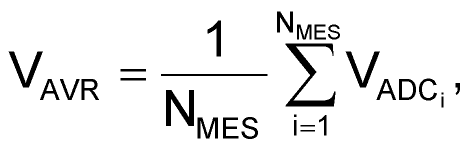(6)

где N_MES – количество результатов измерения АЦП, использованных в расчете. В стабилизаторе GF-9000 в качестве периода измерений удобно было брать период сетевого напряжения, поэтому N_MES ≈ 800 (точное значение зависит от текущего значения частоты сети, и оно постоянно меняется).

При вычислении по формуле (6) самое главное «не вылететь» за пределы разрядности, поскольку при больших значениях N_MES значение суммы может оказаться достаточно большим. Конечно, существуют специальные методы вычислений подобных накопительных сумм с минимальным использованием переменных повышенной разрядности, и они активно используются на 8- и 16-разрядных платформах. Однако для 32-разрядных микроконтроллеров STM32, оснащенных 12-разрядным АЦП, этот вопрос не актуален, поскольку при подобных расчетах в самом худшем случае максимальное значение количества отсчетов намного больше 800:

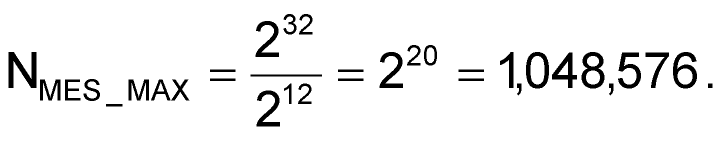(7)

При измерении двуполярных сигналов среднее значение на входе АЦП V_AVR необходимо измерять обязательно. Во-первых, это уменьшает погрешность измерений, во-вторых, позволяет определить наличие и исправность соответствующего датчика. Если V_AVR значительно отличается от 2^{N – 1} (больше чем на 5%), то это в большинстве случаев свидетельствует об аварии в аппаратной части устройства.

При измерении синусоидальных сигналов часто необходимо определять их действующее (среднеквадратическое, эффективное) значение X_RMS. Классическая формула для определения действующих значений периодических сигналов произвольной формы выглядит следующим образом:

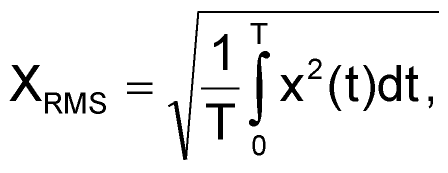(8)

где Т – период сигнала.

Очевидно, что вычисление квадратного корня потребует значительных затрат процессорного времени, даже при наличии в микроконтроллерах STM32 специализированного аппаратного модуля, производящего умножение и деление 32-разрядных чисел за один такт. Тем не менее, как показала практика, необходимости в столь скрупулезном следовании правилам нет, и при синусоидальной форме сигналов величину X_RMS можно с достаточной точностью вычислить на основе средневыпрямленного значения X_ARV по более простой формуле:

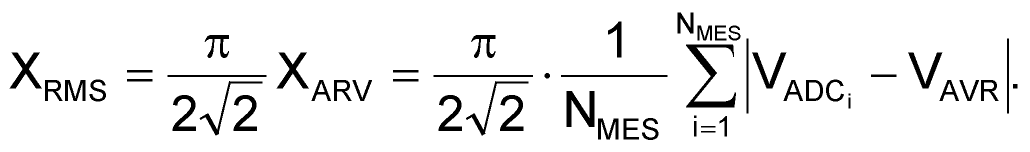(9)

Средневыпрямленное значение X_ARV рассчитывается аналогично среднему значению Х_AVR: вначале формируется сумма модулей, которая затем умножается на соответствующие коэффициенты. При этом на практике оказалось удобнее пользоваться следующей формулой:

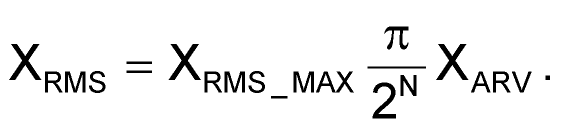(10)

где X_{RMS_MAX} – максимальное действующее значение входного синусоидального сигнала, на которое рассчитан датчик.

Заключение

Цифровые методы позволяют реализовывать очень гибкие алгоритмы управления импульсными преобразователями электрической энергии. В первую очередь это касается сервисных функций, не требующих высокого быстродействия и большого количества вычислений. Однако с каждым днем, по мере появления более скоростных микроконтроллеров, эти методы все больше внедряются в самый важный процесс – процесс преобразования энергии.

Конечной же целью цифровых методов управления станет внутреннее моделирование всех электрических, энергетических и тепловых процессов внутри преобразователя с предсказанием, насколько изменятся ключевые параметры схемы после очередного цикла преобразования. Это необходимо хотя бы для того, чтобы понимать – можно ли этот цикл делать. При этом уже сейчас очевидно, что использование цифровых методов позволяет максимально эффективно использовать силовую часть с одновременным упрощением схемы управления преобразователем.

Список источников

1. Русу А.П. Как управлять импульсными преобразователями с постоянной частотой переключений
2. Русу А.П. Как работают импульсные преобразователи с гистерезисным управлением
3. Русу А.П. Импульсное преобразование переменного тока
4. IGBT-cборки MIPAQPro от Infineon – готовое решение для мощных преобразователей
5. Стабилизатор напряжения импульсный GF-9000
6. Русу А.П. Почему гальваническая развязка увеличивает размеры импульсных преобразователей электрической энергии
7. Указатели на функции (статья с сайта metanit.com)