В перестраиваемых частотно-избирательных RC-цепях частота среза ωC определяется обратной величиной произведения RC, то есть ωC = 1/RC. Если регулировочные элементы представляют собой потенциометры с линейной функциональной характеристикой, у которых R(α) = αRP, где α – нормированное положение ползунка (0 ≤ α ≤ 1), а RP – сопротивление между крайними выводами потенциометра, то частоты среза являются обратными функциями положения движка потенциометра, а шкала частот сжимается в верхней части диапазона регулировки. Такая ситуация обычно нежелательна, поскольку усложняет настройку цепи. Чтобы шкала частот была линейной, необходим управляющий элемент с гиперболической функциональной характеристикой, то есть что-то типа
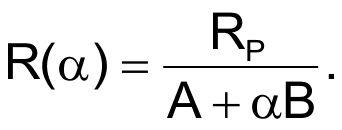
Такие переменные сопротивления обычно не доступны у производителей, но их можно синтезировать, используя потенциометр с линейной функциональной характеристикой и несколько других компонентов.
 |
|
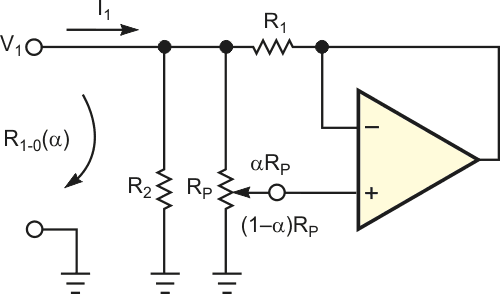
| Рисунок 1. | Эта простая схема синтезирует заземленное переменное сопротивление с гиперболической функциональной характеристикой. |
На Рисунке 1 показана простая схема для создания привязанного к земле переменного сопротивления, имеющего требуемую гиперболическую характеристику управления. Анализ этой схемы дает следующую зависимость сопротивления между узлом 1 и землей от положения элемента управления:
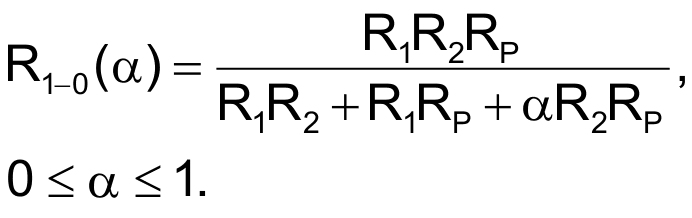
Если последовательно или параллельно с этим сопротивлением включается конденсатор, результирующая частота среза будет линейной функцией α:
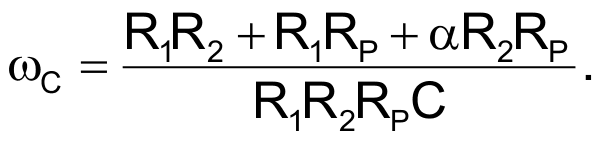
Минимальное и максимальное значения R1-0 составляют
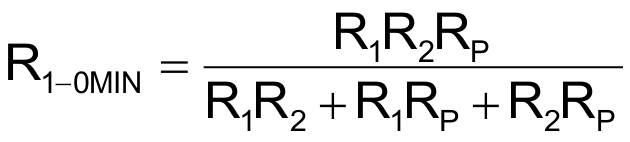
и
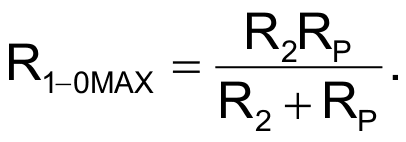
Чтобы разработать эту схему для определенных значений R1-0MIN и R1-0MAX, следует выбрать RP > R1-0MAX и затем рассчитать сопротивления R1 и R2:
и
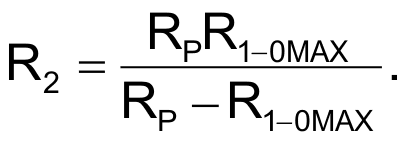
Базовую схему на Рисунке 1 можно расширить, чтобы получить плавающее переменное сопротивление с гиперболической функциональной характеристикой (Рисунок 2). Сопротивление плавающего резистора между узлами 1 и 2 равно
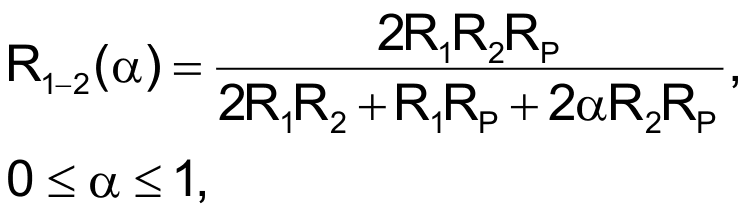
а минимальное и максимальное значения R1-2 равны
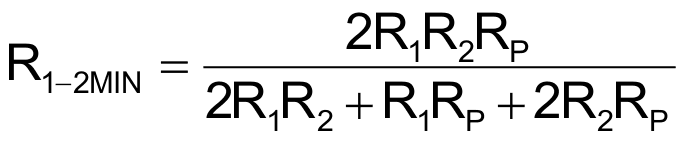
и
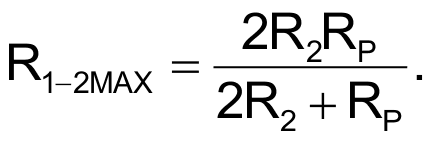
Чтобы сконструировать эту схему для определенных значений R1-2MIN и R1-2MAX, следует выбрать RP > R1-2MAX и затем рассчитать сопротивления R1 и R2:
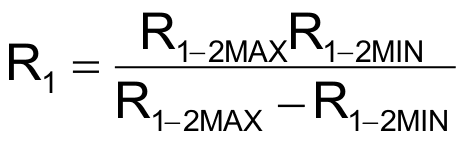
и
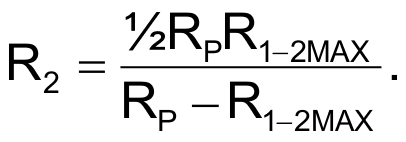
Обратите внимание, что сопротивление резисторов R3 напрямую не влияет на величину R1-2(α). Сопротивления резисторов нужно выбирать достаточно большими, чтобы чрезмерно не перегружать выходы операционного усилителя.
 |
|
| Рисунок 2. | С помощью этой схемы можно реализовать плавающее переменное сопротивление с гиперболической функциональной характеристикой. Обратите внимание, что номиналы резисторов с одинаковыми позиционными обозначениями должны подбираться парами. |
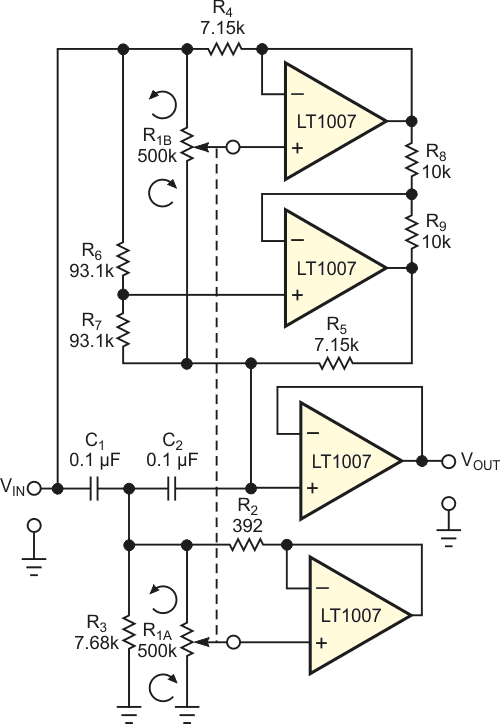
Рисунок 3 иллюстрирует использование схем на Рисунках 1 и 2 в конструкции перестраиваемого мостового Т-образного режекторного фильтра с линейной шкалой частот. Центральная частота режекции фильтра регулируется в диапазоне от 50 до 1000 Гц, а глубина режекции составляет –20 дБ. Из этих требований и при выборе конденсаторов C1 и C2 емкостью 0.1 мкФ следует, что R1-0 изменяется от 375 до 7503 Ом, а R1-2 – от 6752 до 135,047 Ом. (Дополнительным преимуществом использования этого метода является то, что он освобождает разработчика от ограничений конечного числа стандартных номиналов сопротивлений, предлагаемых производителями потенциометров).
 |
|
| Рисунок 3. | В конструкции перестраиваемого мостового Т-образного режекторного фильтра с линейной шкалой частот были использованы базовые схемы на Рисунках 1 и 2. |
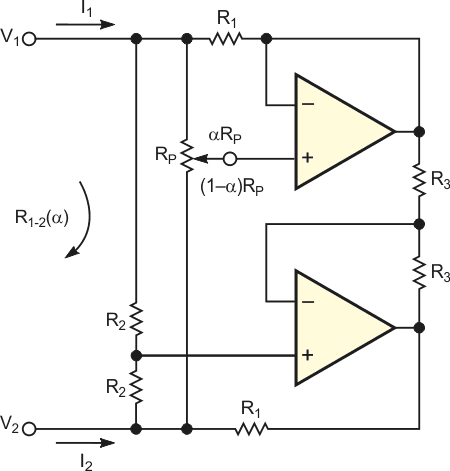
На Рисунке 4 показана смоделированная в Spice зависимость центральной частоты режекции схемы на Рисунке 3 от нормализованного положения движка. Центральная частота режекции является линейной функцией положения регулятора.
 |
|
| Рисунок 4. | Смоделированная в Spice зависимость центральной частоты режекции схемы на Рисунке 3 от нормализованного положения движка показывает, что центральная частота является линейной функцией положения регулятора. |
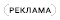
Купить LT1007 на РадиоЛоцман.Цены
