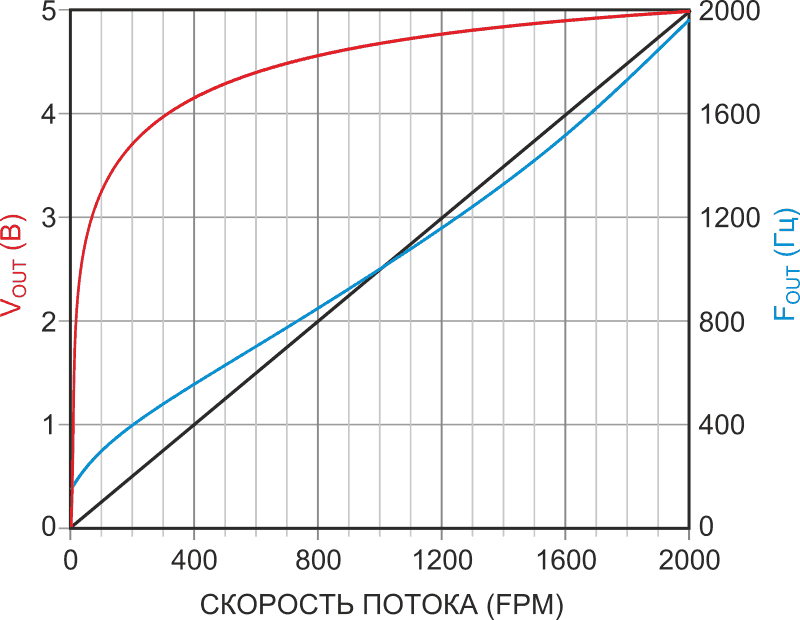
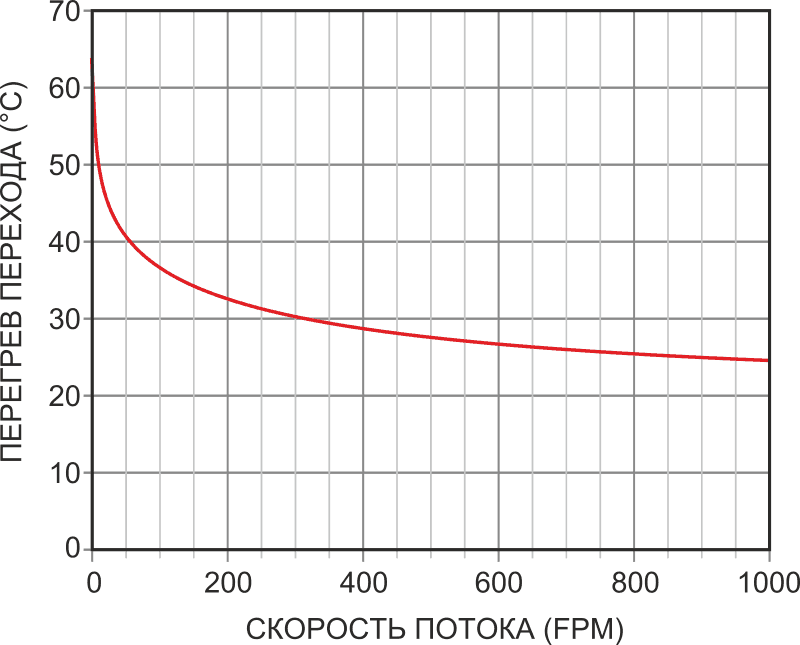
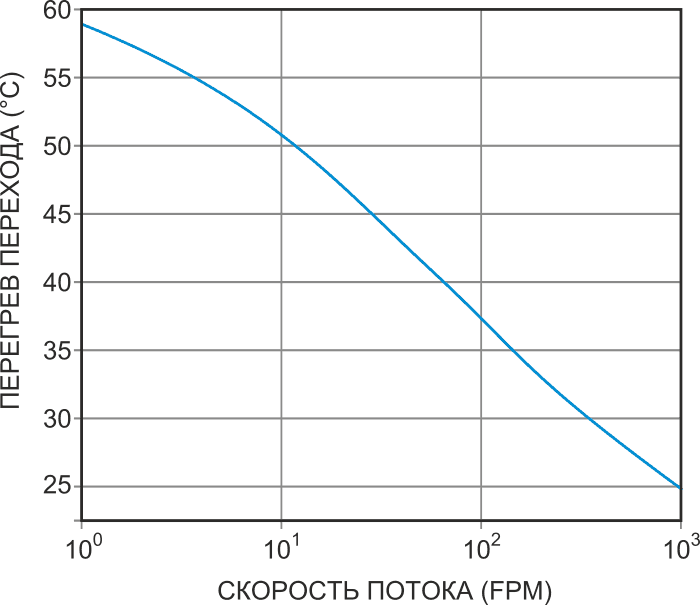
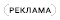Самоподогревающиеся тепловые датчики скорости воздушного потока дешевы, надежны и чувствительны. Однако, как видно из Рисунка 1, они имеют очень нелинейную зависимость температуры датчика от скорости потока (закон Кинга).
 |
|
| Рисунок 1. | Изменение температуры перехода транзистора в корпусе TO-92 при рассеиваемой мощности 320 мВт показывает нелинейную зависимость между воздушным потоком и температурой датчика. |
Кривая на Рисунке 1 соответствует приведенной ниже эмпирической формуле, связывающей температуру перехода с рассеиваемой мощностью и скоростью воздушного потока для самоподогревающегося транзистора в корпусе TO-92:
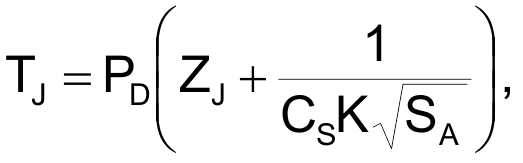
где:
TJ – перегрев перехода относительно температуры окружающей среды (°C),
PD – мощность, рассеиваемая на переходе (Вт),
ZJ – тепловое сопротивление переход-корпус (44 °C/Вт),
CS – теплопроводность корпус-окружающая среда в неподвижном воздухе (6.4 мВт/°C),
K – константа термодиффузии закона Кинга (0.75 мВт/°C/√fpm),
SA – скорость потока воздуха в футах в минуту (feet per minute, fpm).
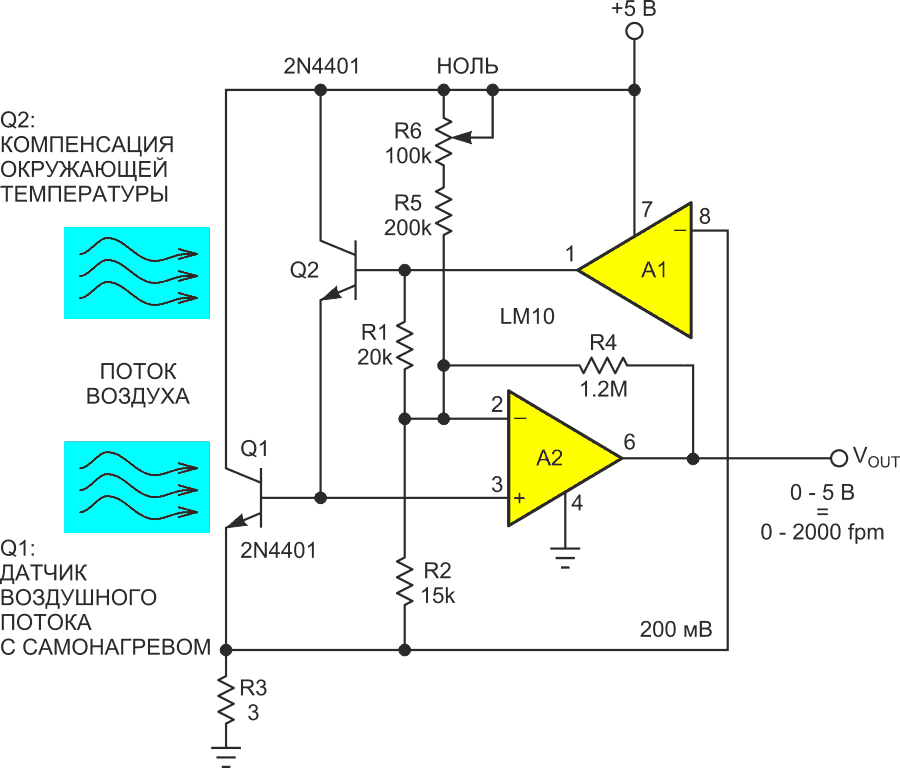
На Рисунке 2 показана практическая схема термодатчика, сделанная на основе транзисторной пары Дарлингтона Q1 и Q2.
 |
|
| Рисунок 2. | Самоподогревающийся тепловой датчик скорости воздушного потока на основе пары Дарлингтона. |
Q1 выполняет роль самоподогревающегося датчика. Температурный коэффициент его напряжения база-эмиттер преобразует температуру в напряжение с коэффициентом –1.5 мВ/°C. Напряжение 200 мВ опорного источника A1 (LM10) стабилизирует ток транзистора Q1 на уровне 0.2 В/R3 = 67 мА, поддерживая мощность, рассеиваемую Q1, постоянной и равной 67 мА × 4.8 В = 320 мВт. Результирующая разность температур окружающей среды и перехода обеспечивает показания скорости воздушного потока при охлаждении с 64 °C при 0 fpm до 22 °C при 2000 fpm с соответствующим увеличением напряжения база-эмиттер на 63 мВ с 654 мВ при 0 fpm до 717 мВ при 2000 fpm.
При этом транзистор Q2 обеспечивает независимую от скорости потока компенсацию температуры окружающей среды.
Обратная связь через резистор R4 и соответствующую цепочку резисторов устанавливает масштабный коэффициент 0–2000 fpm = 0–5 В, а резистор R6 обеспечивает регулировку нуля при отсутствии воздушного потока. Но для того, чтобы преобразование и получение сигнала скорости потока было осмысленным, необходимо что-то сделать с этой отвратительной нелинейностью.
Рисунок 3 – это то, что нужно.
 |
|
| Рисунок 3. | Показан нелинейный ПНЧ на основе таймера 555, сконфигурированного в автоколебательной топологии, и резисторной цепочки, подк люченной к VIN, что обеспечивает решение проблемы предыдущей нелинейности. |
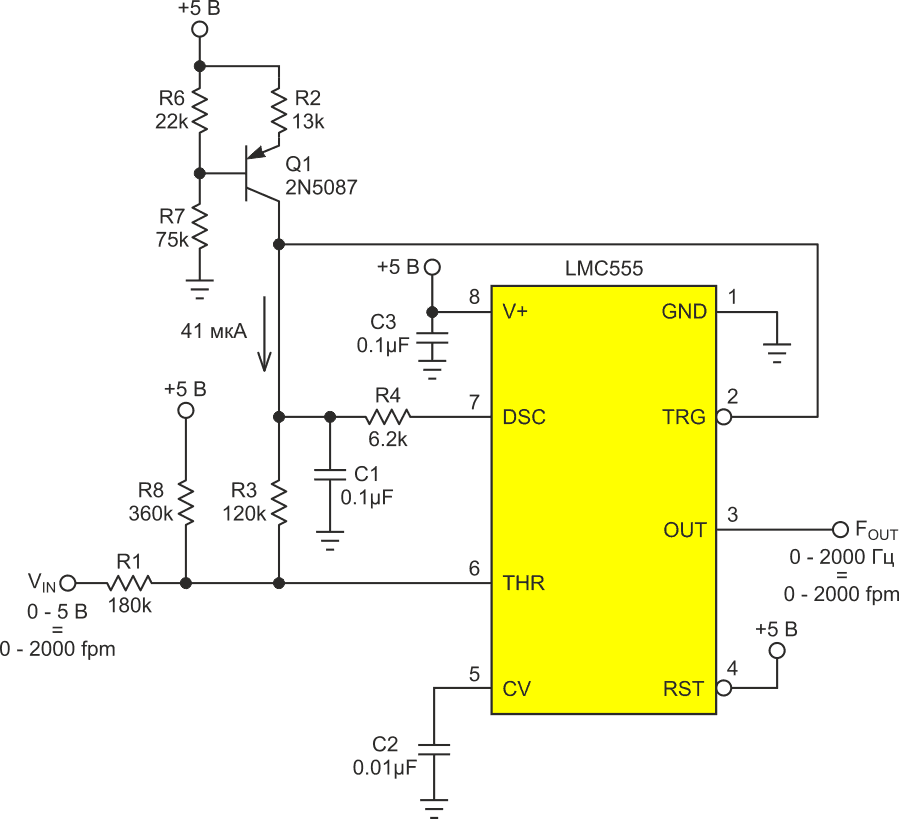
Таймер U1 включен по довольно типичной автоколебательной схеме, за исключением того, что подключенная к VIN цепочка резисторов смещает напряжение VTHR на выводе THR пропорционально напряжению VIN. В результате при изменении входного напряжения VIN от 0 до 5 В, что соответствует изменению скорости потока от 0 до 2000 fpm, максимумы пилообразного напряжения VTHR начинают смещаться чуть выше порога 2/3V+ (соответствующего примерно 0 Гц), в то время как минимумы приближаются к этому пределу (соответствующему примерно 2000 Гц). Таким образом, по мере увеличения VIN в ответ на увеличение скорости воздушного потока, амплитуда пилообразного напряжения на выводе 6 неуклонно уменьшается. Это увеличивает зависимость частоты от скорости потока, компенсируя противоположное поведение закона Кинга (красная кривая на Рисунке 4).
 |
|
| Рисунок 4. | Линеаризованный с помощью ПНЧ отклик на скорость воздушного потока (синяя кривая). Теперь увеличение зависимости частоты от скорости потока компенсирует эффект закона Кинга (красная кривая), чтобы получить 1 Гц = 1 fpm. |
Полученная в результате сильно нелинейная кривая преобразования напряжения в частоту (ПНЧ) обеспечивает разумную компенсацию линейности сильно нелинейного отклика датчика на Рисунке 2, как показывает синяя кривая на Рисунке 4, чтобы достичь окончательной калибровки 1 Гц = 1 fpm.
Наконец, вероятно, нуждается в пояснении источник тока на p-n-p транзисторе Q1 на Рисунке 3. Влияние температурного коэффициента напряжения база-эмиттер –2 мВ/°C в сочетании с резисторами, окружающими транзистор, приводит к тому, что его ток коллектора имеет температурный коэффициент примерно +0.3%/°C, что, казалось бы, плохо для точности преобразования. Но все как раз наоборот; температурный коэффициент Q1 повышает точность измерения скорости воздушного потока, компенсируя изменение плотности воздуха в зависимости от температуры.
Согласно древнему закону идеального газа Клапейрона 1834 года (PV = nRT), плотность воздуха (число молекул на единицу объема n/V) и, следовательно, теплоемкость на единицу объема обратно пропорциональна абсолютной температуре (n/V = P/(RT)). Поэтому точное измерение скорости воздушного потока, пропорциональной объему воздуха, подразумевает прямую зависимость от абсолютной температуры, которая при «комнатной» температуре характеризуется коэффициентом +0.3%/°C. Повышение температуры окружающей среды приводит к росту тока коллектора Q1, что увеличивает частоту колебаний U1 в соответствии именно с этим коэффициентом.
Итак. Честь и хвала транзистору Q1!
ДОПОЛНЕНИЕ
Умный комментарий дал Константин Ким:
Рисунок1 выглядит вполне линейным на полулогарифмической шкале (Рисунок 5).
 |
|
| Рисунок 5. | Кривая Константина Кима. |
Действительно, так оно и есть! Это навело на мысль, что относительно простая антилогарифмическая схема могла бы приемлемо выполнить работу по выпрямлению сильно изогнутой кривой отклика на скорость воздушного потока на Рисунке 1, и сделать это с гораздо меньшим количеством произвольных манипуляций и ухищрений, чем в несколько бессистемном подходе, показанном на Рисунке 3.
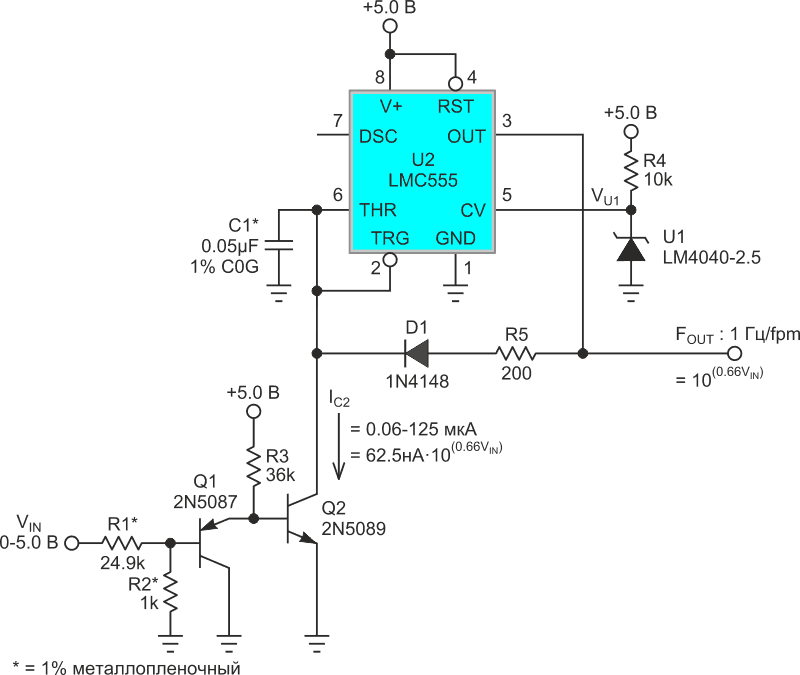
Поэтому я сразу же начал строчить и рисовать антилогарифмы. Получившаяся в результате схема показана на Рисунке 6.
 |
|
| Рисунок 6. | Антилогарифмически нелинейный преобразователь напряжение-частота. |
Транзисторы Q1 и Q2 образуют комплементарную пару Дарлингтона, в которой равные, но противоположные по знаку прямые смещения (то есть, напряжения переходов база-эмиттер p-n-p и n-p-n транзисторов) обнуляют соответствующие напряжения смещения и температурные зависимости так, что:
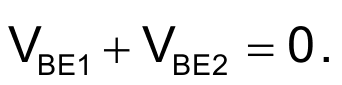
Это позволяет воспользоваться антилогарифмической зависимостью тока коллектора транзистора Q2 от входного напряжения VIN.
 |
|
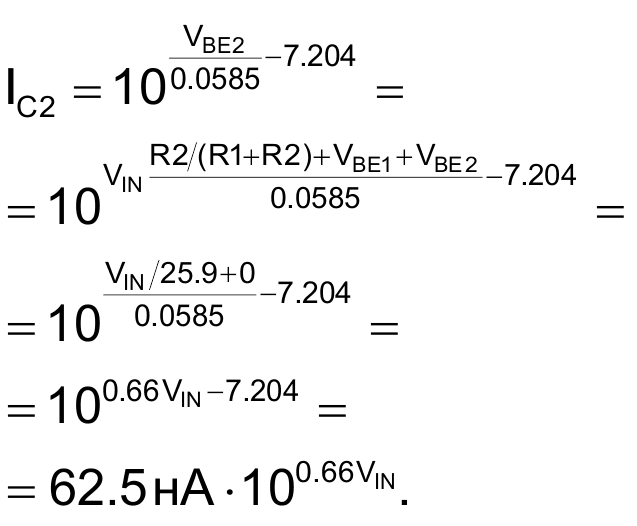
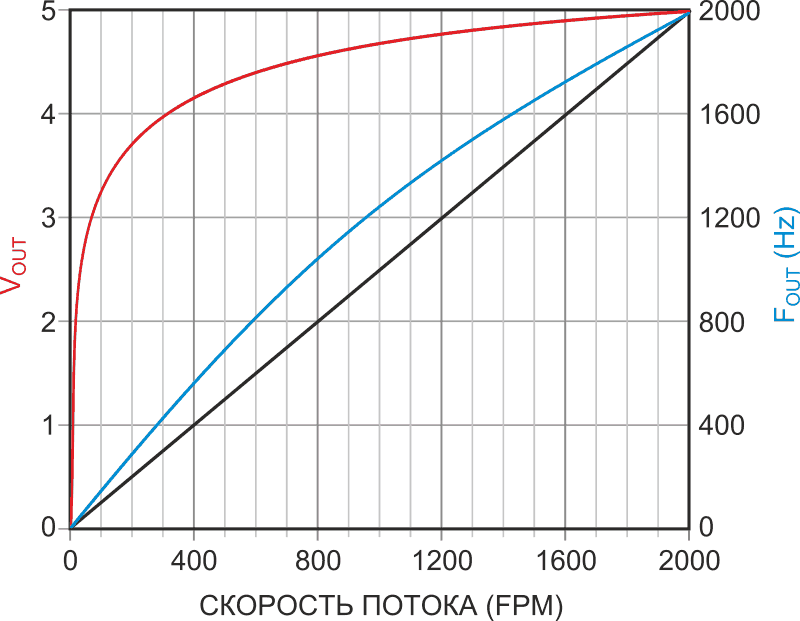
| Рисунок 7. | Антилогарифмическая линеаризация датчика скорости воздушного потока на транзисторе Дарлингтона.. |
Использование результирующего тока для разряда времязадающего конденсатора C1 формирует пилообразное напряжение, наклон которого прямо пропорционален скорости воздуха и частоте колебаний преобразователя напряжение-частота:
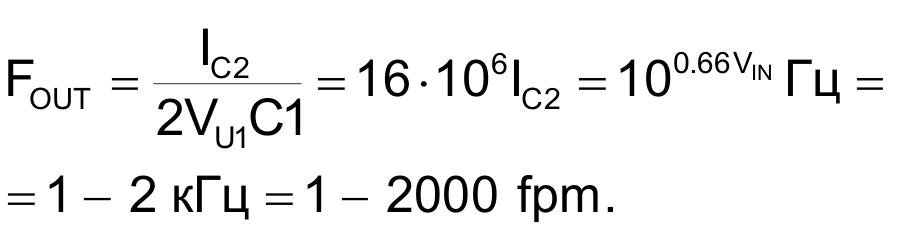
Результат показан на Рисунке 7 (синяя кривая).
Честь и хвала Константину Киму!
